- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
Edexcel IGCSE Maths 复习笔记 3.11.1 Differentiation - Basics
Edexcel IGCSE Maths 复习笔记 3.11.1 Differentiation - Basics
What is differentiation?
- Differentiation is part of the branch of mathematics called Calculus
- It is concerned with the rate at which changes takes place – so has lots of real‑world uses:
- The rate at which a car is moving – ie. its speed
- The rate at which a virus spreads amongst a population
- To begin to understand differentiation you’ll need to understand gradient
Gradient
- Gradient generally means steepness.
- For example, the gradient of a road up the side of a hill is important to lorry drivers
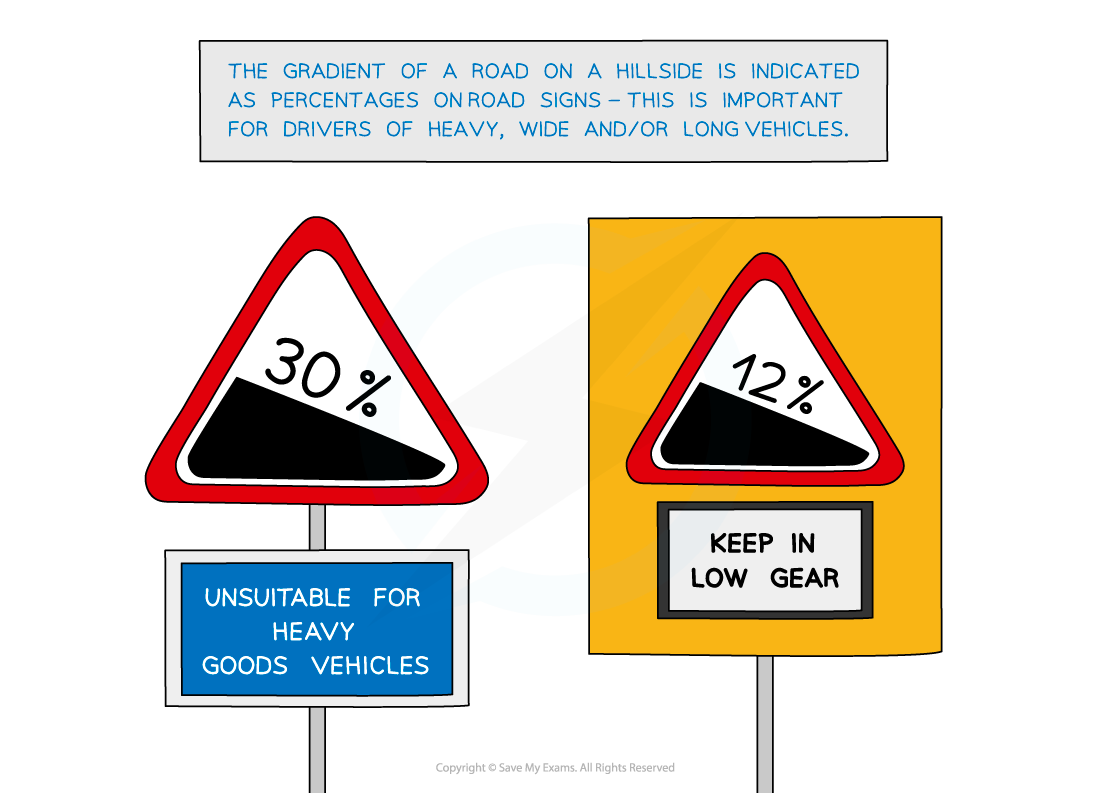
- On a graph the gradient refers to how steep a line or a curve is
- It is really a way of measuring how fast y changes as x changes
- This may be referred to as the rate at which y changes
- So gradient is a way of describing the rate at which change happens
Straight lines and curves
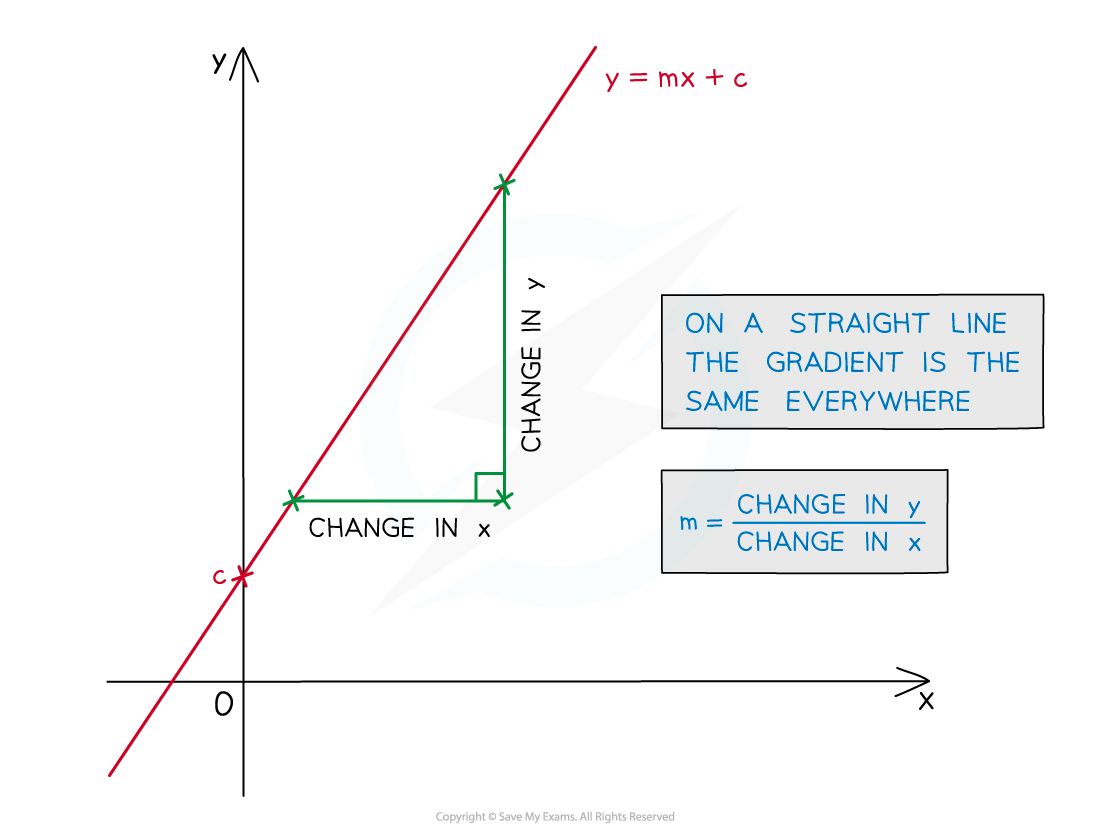
- For a straight line the gradient is always the same (constant)
- Recall y= mx + c, where m is the gradient (see Straight Lines - Finding Equations)
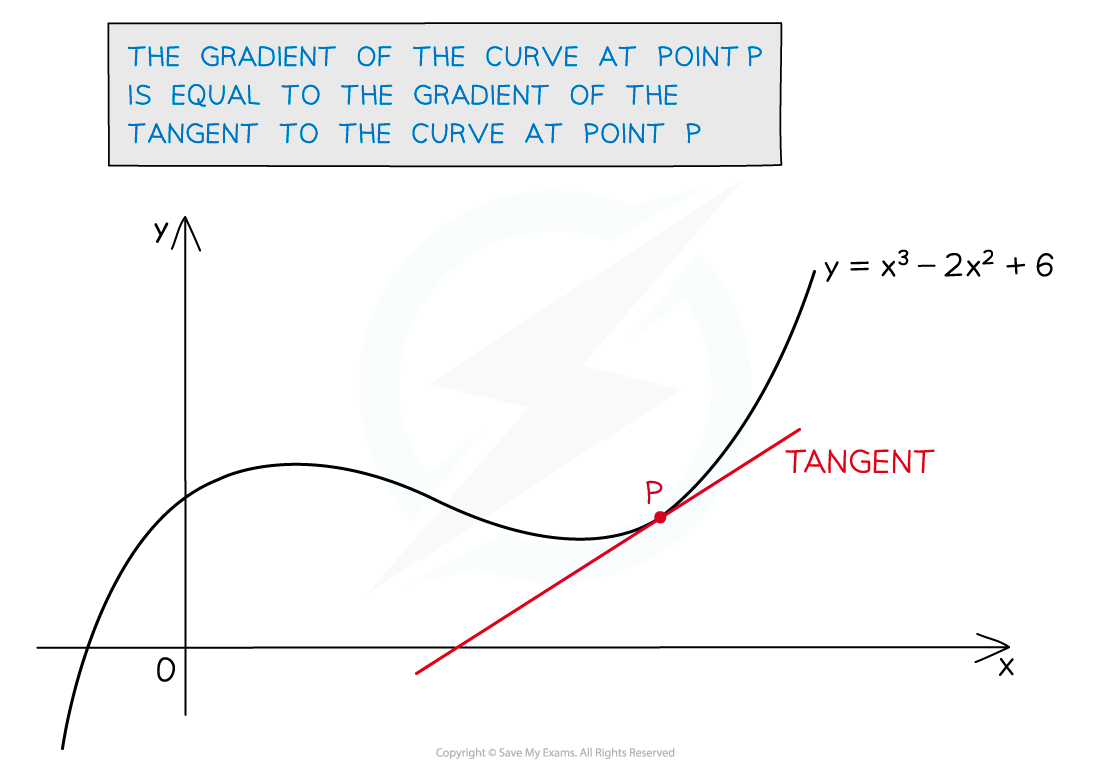
- For a curve the gradient changes as the value of x changes
- At any point on the curve, the gradient of the curve is equal to the gradient of the tangent at that point
- A tangent is a straight line that touches the curve at one point
- The gradient function is an expression that allows the gradient to be calculated anywhere along a curve
- The gradient function is also called the derivative
How do I find the gradient function or derivative?
- This is really where the fun with differentiation begins!
- The derivative (dy/dx) is found by differentiating y
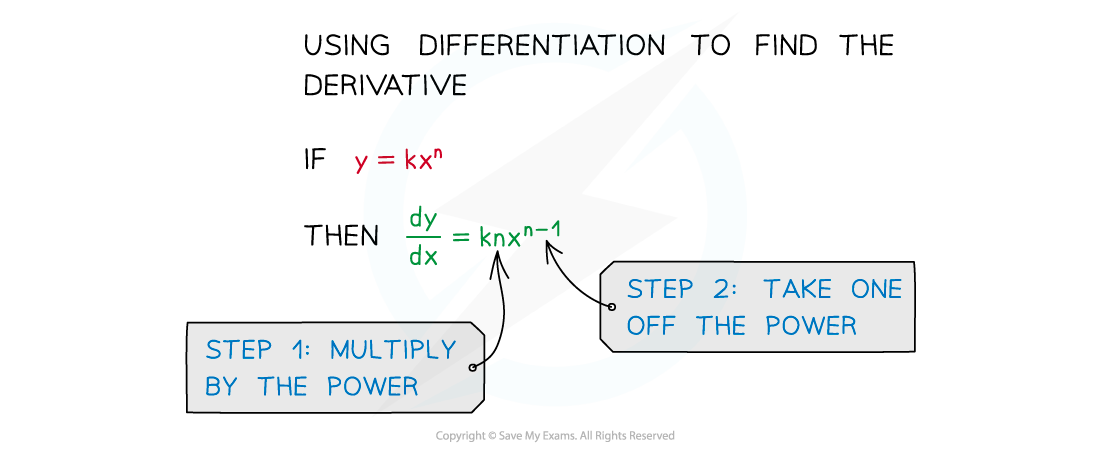
- This looks worse than it is!
- For powers of x ...
- STEP 1 Multiply by the power
- STEP 2 Take one off the power

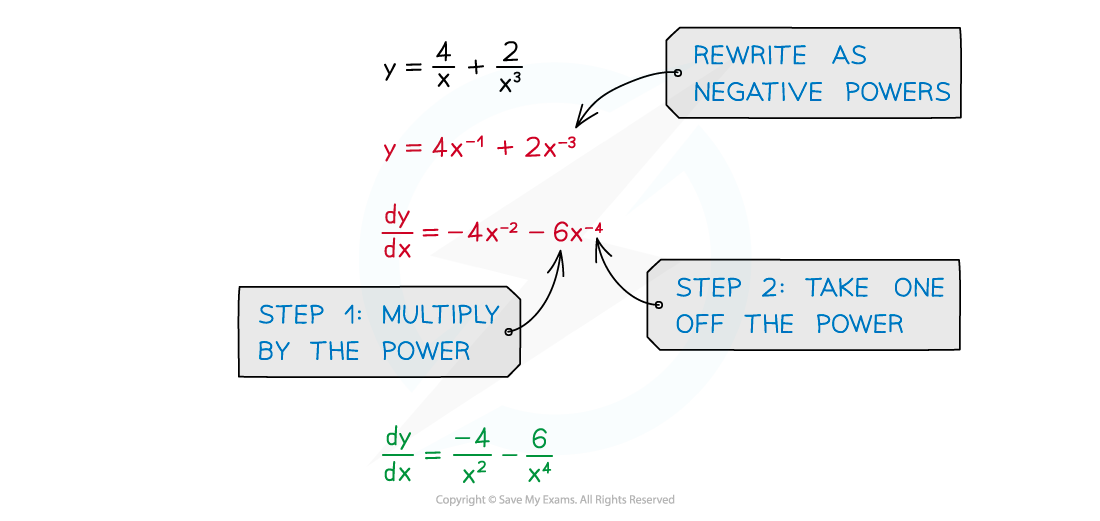
- This method applies to positive and negative integers
- Negative powers arise with fractions and reciprocals
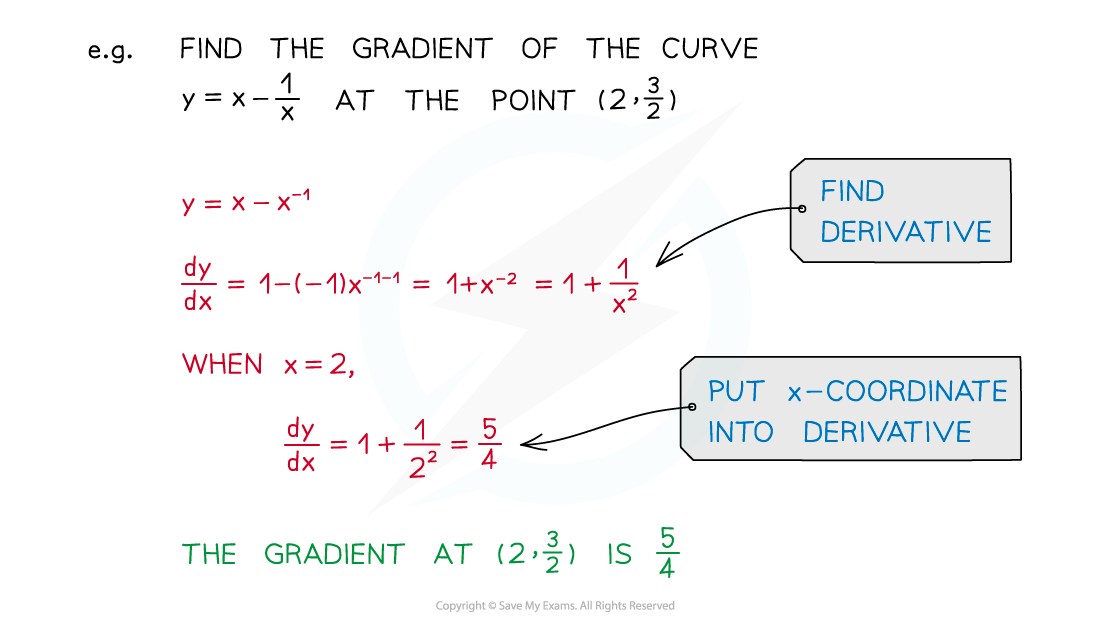
How do I find the value of a gradient?
- Substitute the x value into the expression for the derivative, and evaluate it
Exam Tip
When differentiating long, awkward expressions write each step out fully and simplify afterwards.Take extra care when differentiating negative powers of x
Worked Example
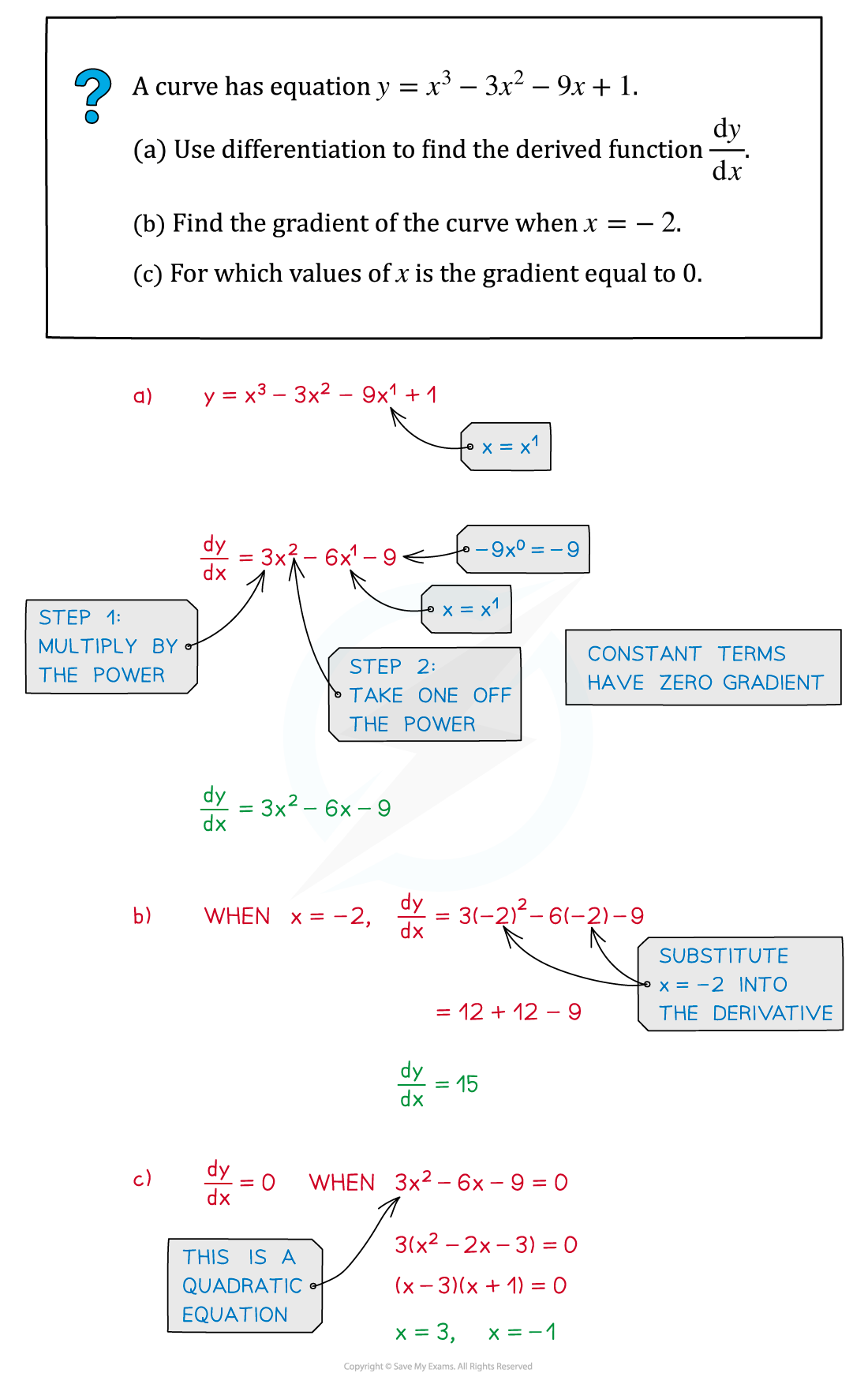
转载自savemyexam
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





