- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
Edexcel IGCSE Maths 复习笔记 3.8.1 Transformations of Graphs
Edexcel IGCSE Maths 复习笔记 3.8.1 Transformations of Graphs
What are graph transformations?
- You should have come across transformations of shapes – reflections, rotations, translations and enlargements
- These are often performed on 2D coordinate grids (and can be applied in 3D too)
- Therefore it is possible to transform graphs as they are also drawn on 2D coordinate grids
- Graph transformations are described differently to transforming shapes
- In general, a graph can be considered as having the equation y = f(x) ...
- ... where f(x) will be some expression involving x
- At IGCSE graph transformations cover:
- linear functions f(x) = mx + c
- quadratic functions f(x) = ax2 + bx +c
- f(x) = sin x
- f(x) = cos x
- In fact many exam questions do not state the actual function!
- A graph is provided with it being referred to just as y = f(x)
- It will be impossible to tell what f(x) is from the graph
- But some key points will be highlighted

Graph Translations f(x+a) and f(x)+a
- f(x + a) translates the graph -a units in the positive x direction (‘right’)
- f(x – a) translates the graph a units in the negative x direction (‘left’)
- Notice the opposite signs!
- f(x) + a translates the graph a units in the positive y direction (‘up’)
- f(x) – a translates the graph a units in the negative y direction (‘down’)

- There is a logic to these but the easiest way is to memorise and recognise them
- With y = f(x) ± a the “±a” happens after the function
- So the ‘output’ of the function changesie. y-coordinates change
- With y = f(x ± a) the “±a” happens before the function
- So the ‘input’ of the function changesie. x-coordinates change
- These second translations may seem as though they are in the wrong direction
- In the case of “+a” the ‘input’ will be greaterso the graph happens “sooner”
ie. graph moves left
- In the case of “-a” the ‘input’ will be smaller
so the graph happens “later”ie. graph moves right
- In the case of “+a” the ‘input’ will be greaterso the graph happens “sooner”

Graph Stretches f(ax) and af(x)
- f(ax) is a horizontal stretch by a scale factor of 1/a
- May also be referred to as a stretch in (or parallel to) the x-direction
- This looks like a “squash” but that is not a technical term – do not use it!
- af(x) is a vertical stretch by a scale factor of a
- May also be referred to as a stretch in (or parallel to) the y-direction

- There is a logic to these as well but memory and recognition is easier!
- With y = af(x) the “a” happens after the function
- So the ‘output’ of the function changesie. y-coordinates change
- With y = f(ax) the “a” happens before the function
- So the ‘input’ of the function changesie. x-coordinates change
- This stretch may seem it has the wrong scale factor (1/a)
- However the ‘input’ is being multiplied by a – so x will need to be divided by a in order for the function to receive the same input

Special cases – graph reflections f(-x) and -f(x)
- f(-x) and -f(x) are of the form of stretches (a = -1) but lead to special cases that are easiest dealt with separately
- f(-x) is a reflection in the y-axis
- -f(x) is a reflection in the x-axis

- Yes, there is a logic to these too but as before it is easier to memorise them
- With y = -f(x) the “-” happens after the function
- So the ‘output’ of the function changes ie y-coordinates change sign
- y-coordinates changing sign means a reflection in the x-axis
(Think about it or draw a diagram if you’re not yet convinced!)
- With y = f(-x) the “a” happens before the function
- So the ‘input’ of the function changes ie x-coordinates change sign
- x-coordinates changing sign means a reflection in the y-axis(Go on, draw a diagram!)

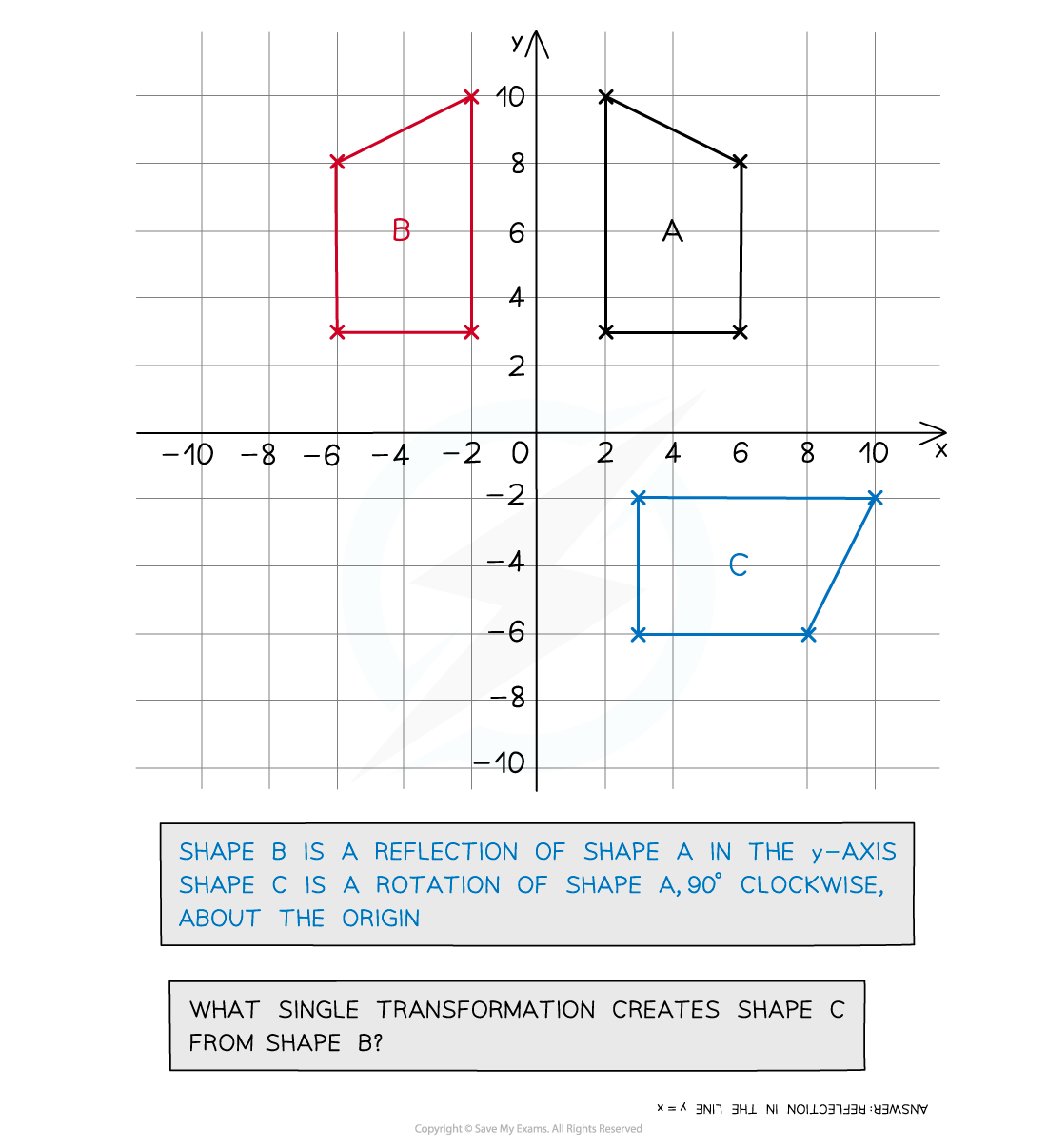
Recognising graph transformations?
- So far all examples have involved sketching a graph for a given transformation
- However some questions ask for a description of the transformation having provided both the original and transformed graphs
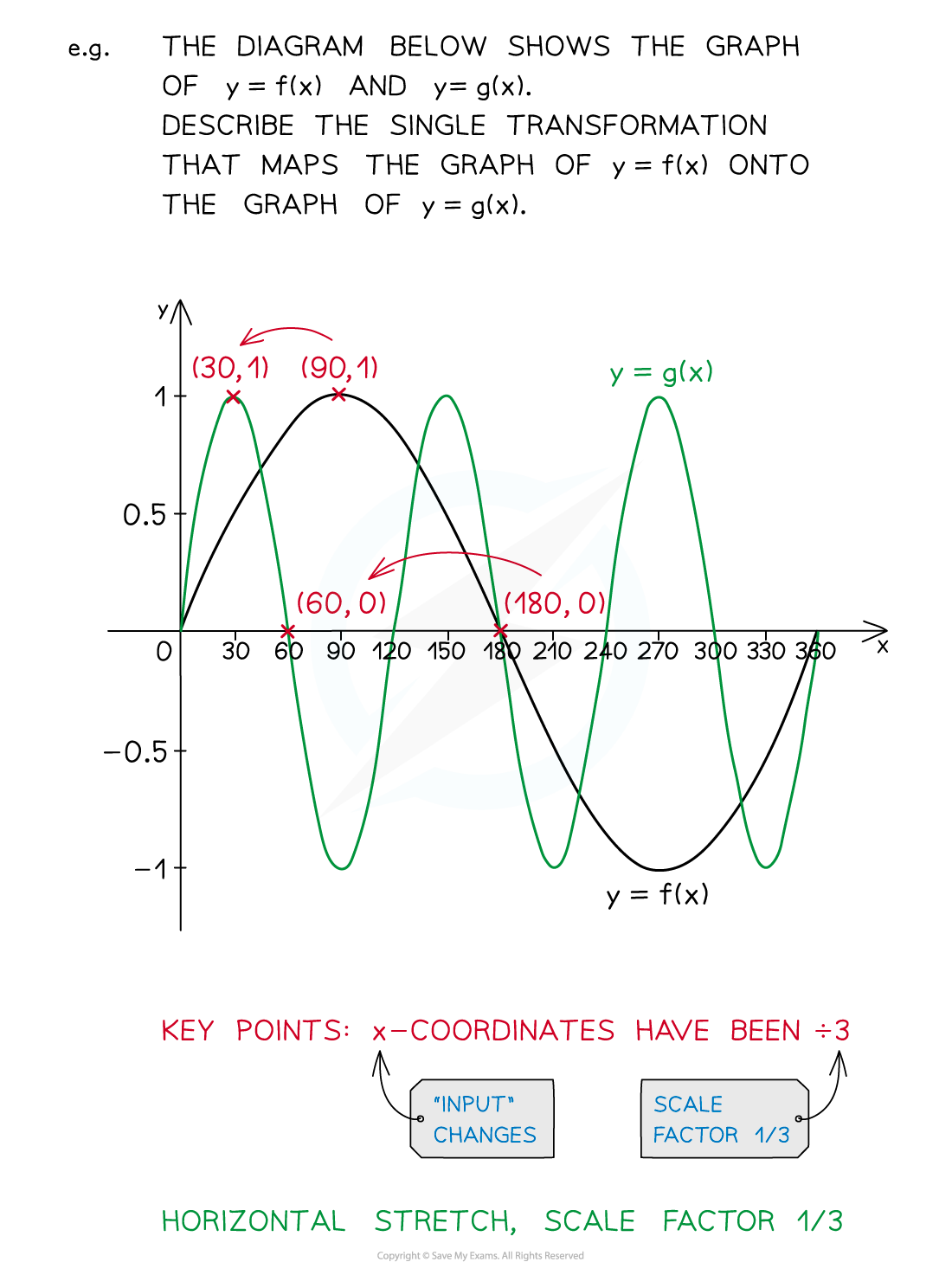
Exam Tip
If not mentioned in the question, look for key points on the graph to transform where the graph crosses the x- and/or y- axes and any turning points that have obvious coordinates.Once the key points have been transformed it is usually easy to complete the rest.Some questions may only ask you about what happens to certain points and not the whole graph.
Worked Example
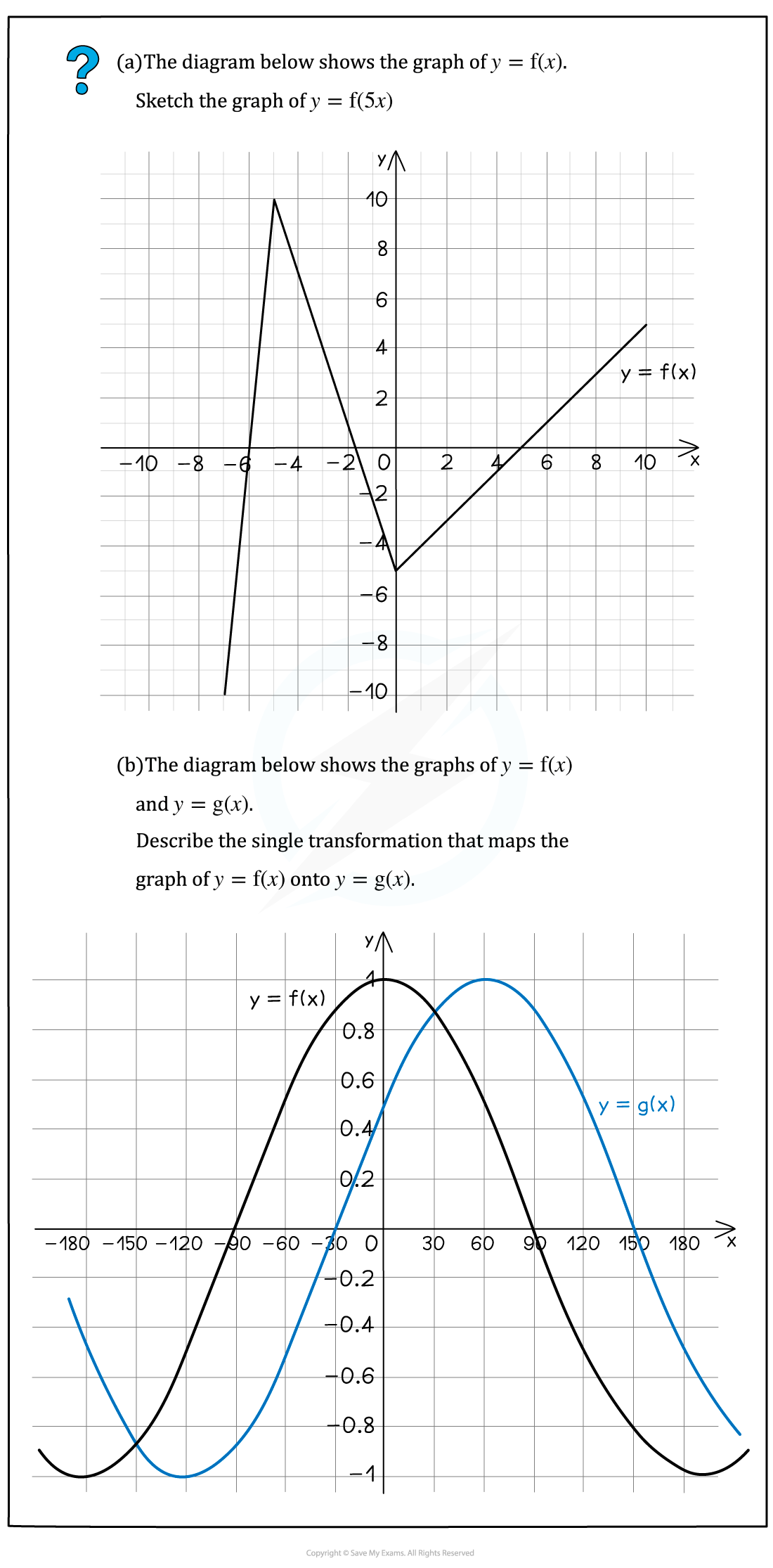
Worked Example
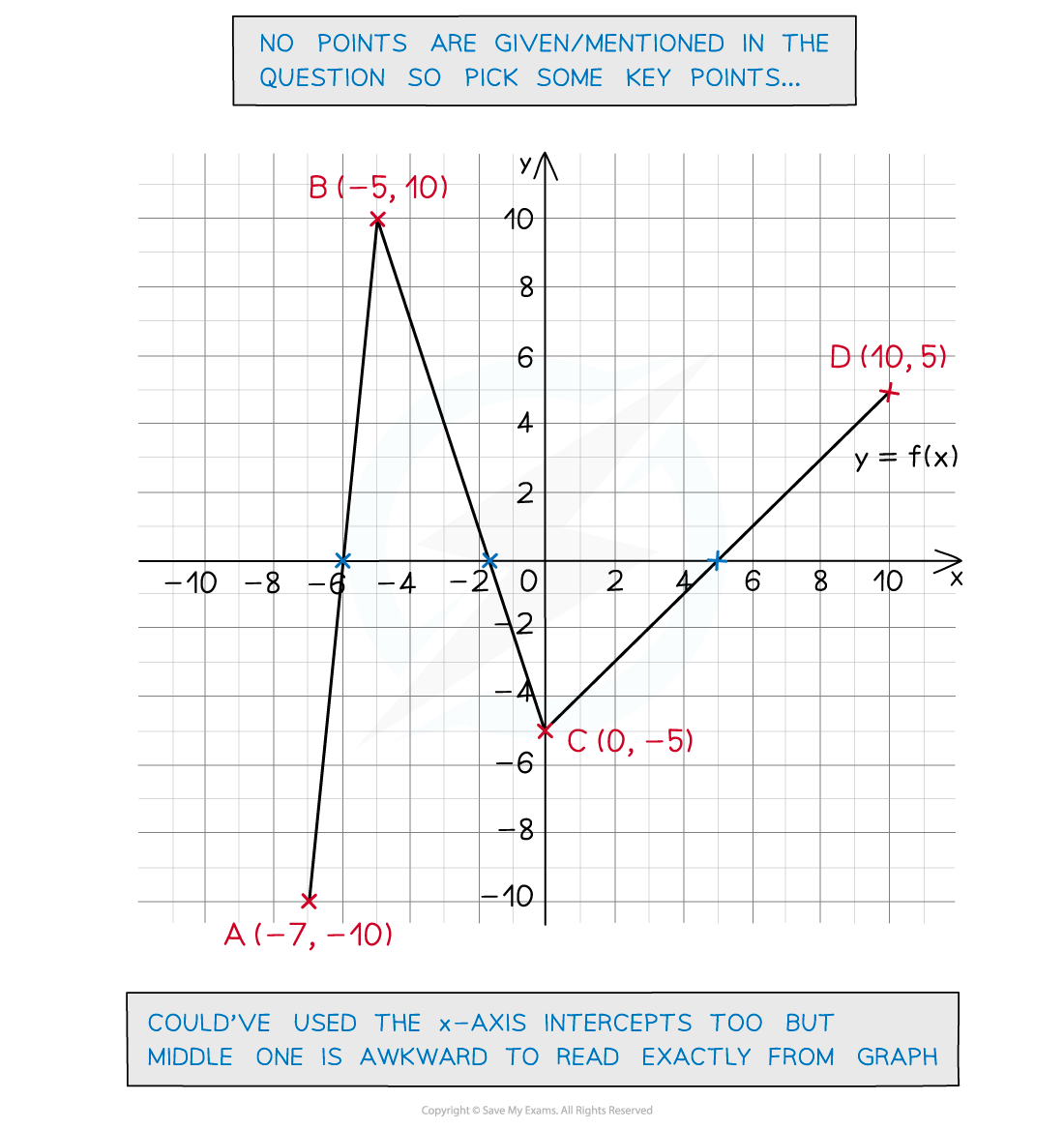
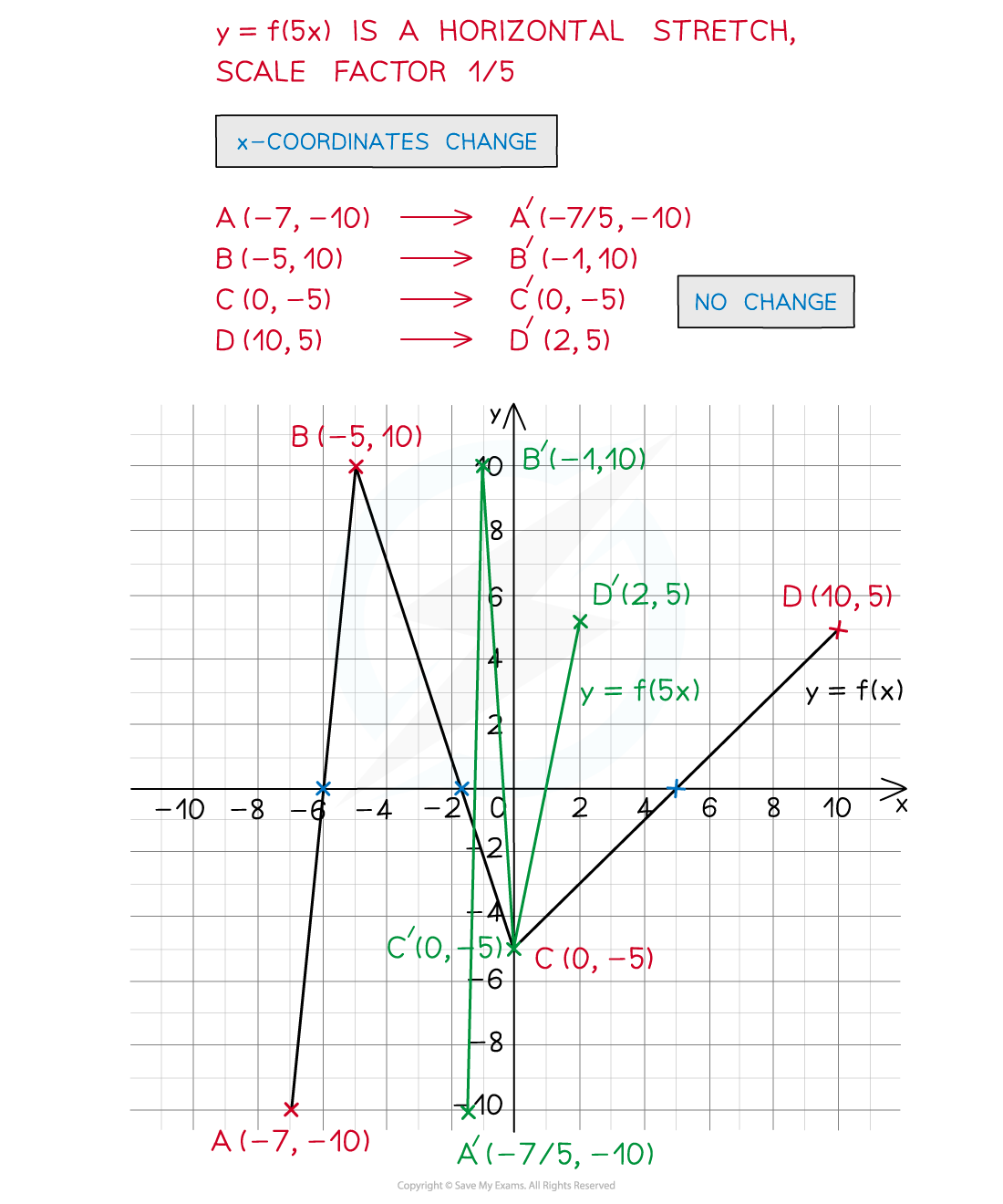
Worked Example
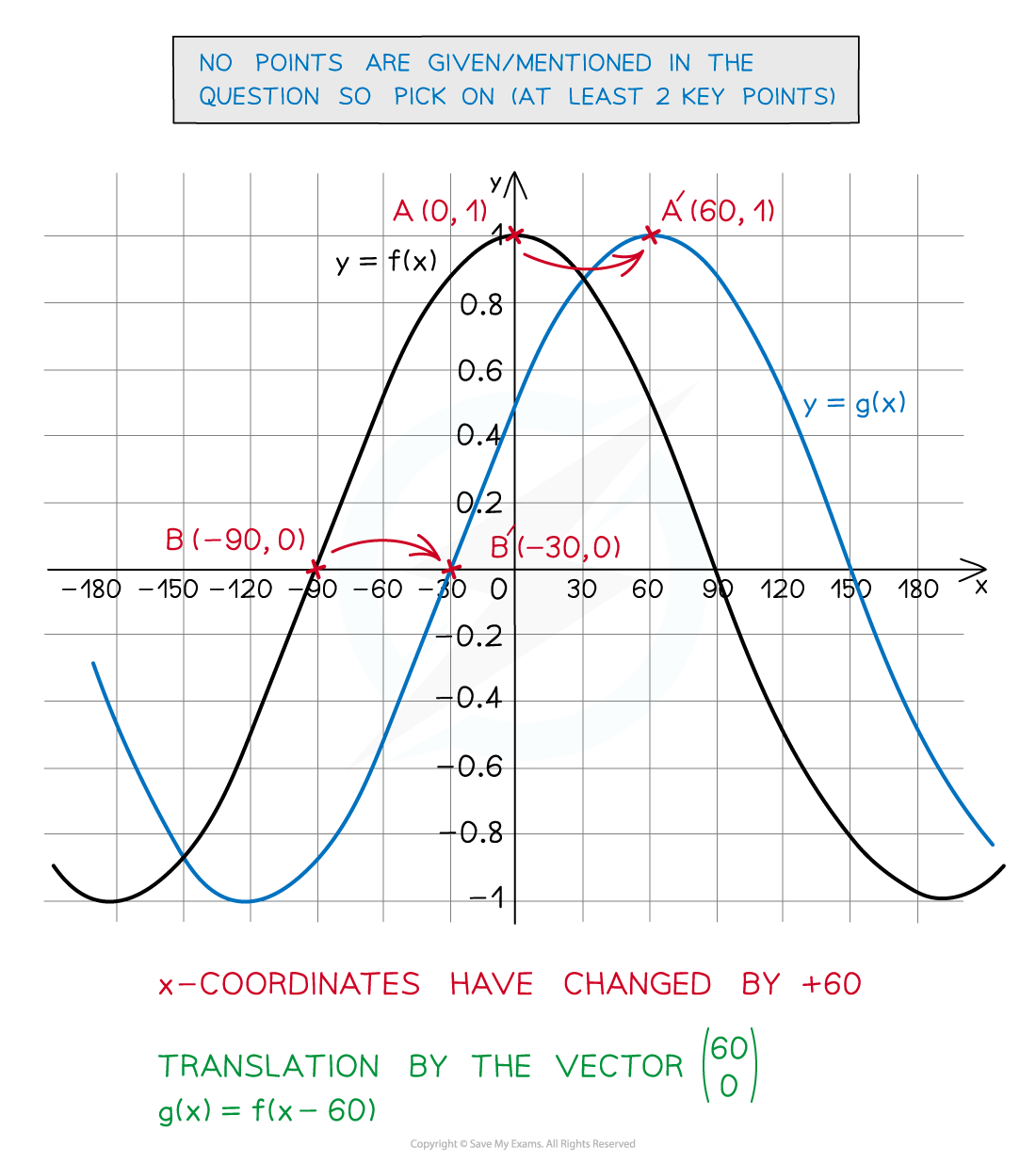
转载自savemyexam
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





