- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
Edexcel IGCSE Maths 复习笔记 3.2.4 Functions - Domain, Range & Exclusions
Edexcel IGCSE Maths 复习笔记 3.2.4 Functions - Domain, Range & Exclusions
What are functions?
- Functions are a formal way of writing mathematical expressions
- eg. f(x) = 3x + 2 would be a linear function
- eg2. g : x ⟼ x2 + 3x – 5 would be a quadratic function

What is the domain of a function?
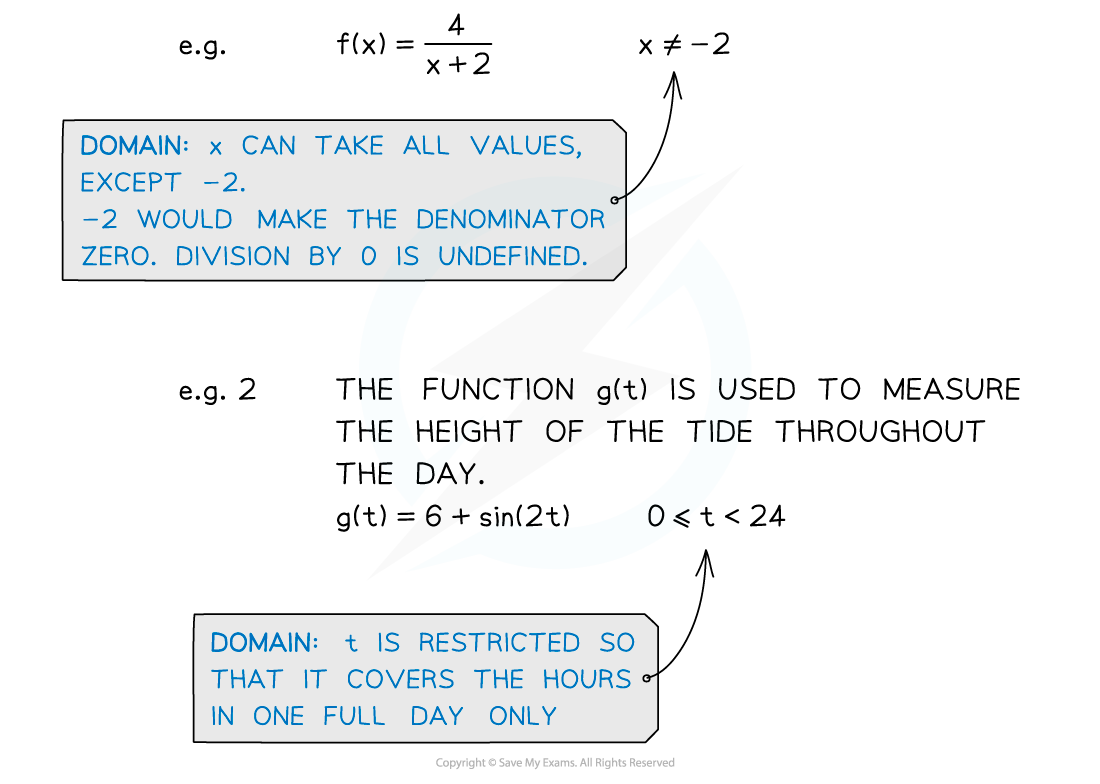
- The domain of a function is the values of x (the “input”) are allowed to take
- For some functions, x cannot be certain values
- eg. f(x) = 1 / xx cannot take the value 0
- Other times we may choose to restrict the values of x
- eg. The function g(x) = 5 – 2x2 is used to model the height of water throughout the day where x indicates timeIt may make sense to limit x so it only covers a 24 hour period
- Inequalities are used to describe the values x can take
- Any exclusions are usually indicated using the “not equal to” symbol (≠)
What is the range of a function?
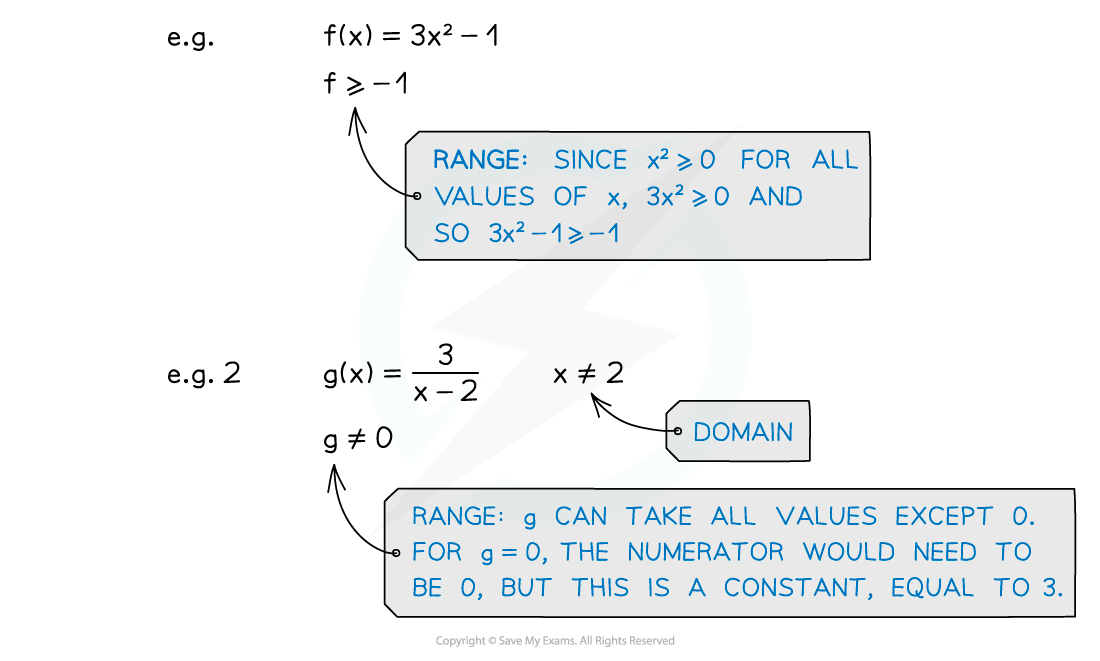
- The range of a function is the values of f (the “output”) that could occur
- Some functions can never take certain values, regardless of the value of x
- eg. f(x) = x2f, a squared (real) value, cannot be negative
- eg2. g(x) = 1 / xg can never be zero (because numerator cannot be 0)
- The range of a function can be influenced by its domain
- As with the domain, inequalities are used to describe the values a function can take and “not equal to” (≠) is used for any exclusions
How do I solve problems involving the domain and range

- You need to be able to identify and explain any exclusions in the domain of a function
- You need to be able to deduce the range of a function from its expression and domain
- You may also be asked to sketch a graph of a function
- This could involve sketching parts of familiar graphs that are restricted because of the domain and exclusions

Domain and range of inverse functions
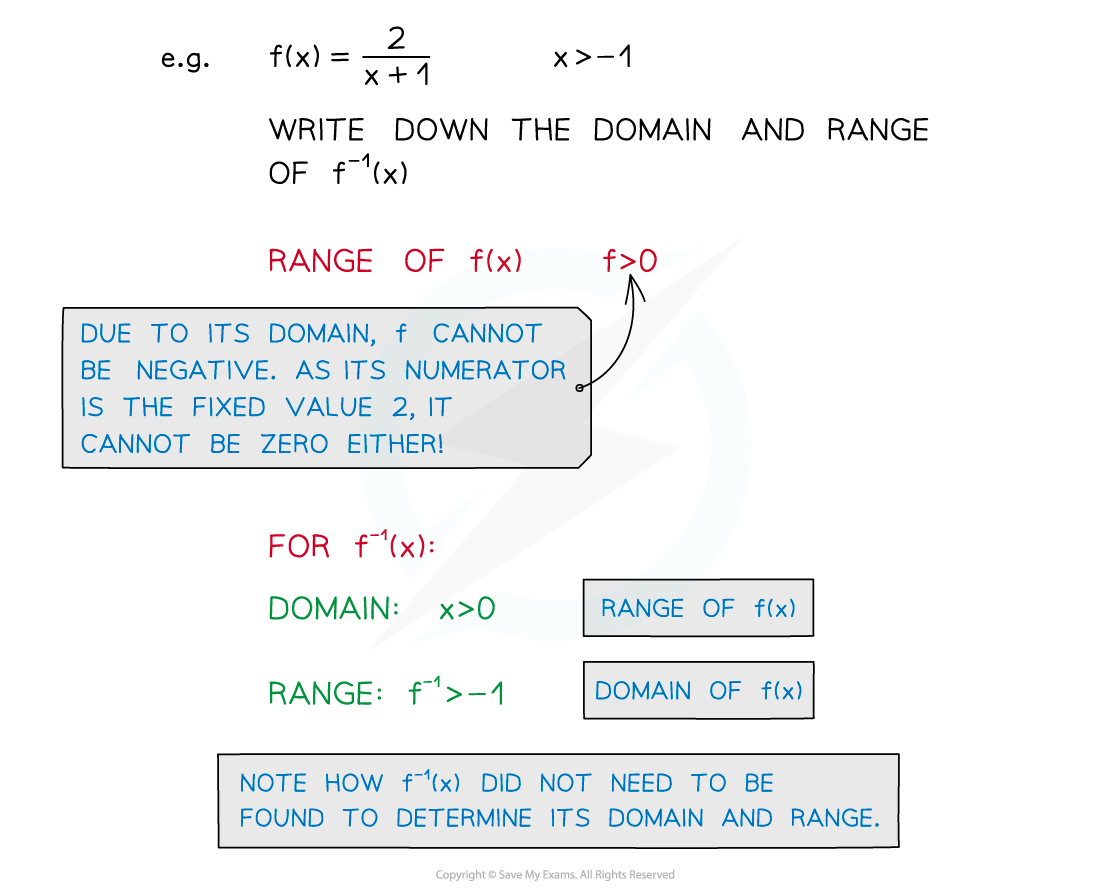
- Make sure you are familiar with inverse functions, denoted by f-1, g-1, etc.
- The range of a function is the domain of the inverse function
- The domain of a function is the range of the inverse function
Exam Tip
A graph of the function can help “see” both the domain and range of function, and a sketch can help if you have not been given a diagram.
Worked Example

转载自savemyexam
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





