Edexcel IGCSE Maths 复习笔记 3.1.3 Arithmetic Sequences - Sum of n terms
What is an arithmetic sequence or arithmetic series?
- Ensure you are familiar with Sequences – Basics and Linear
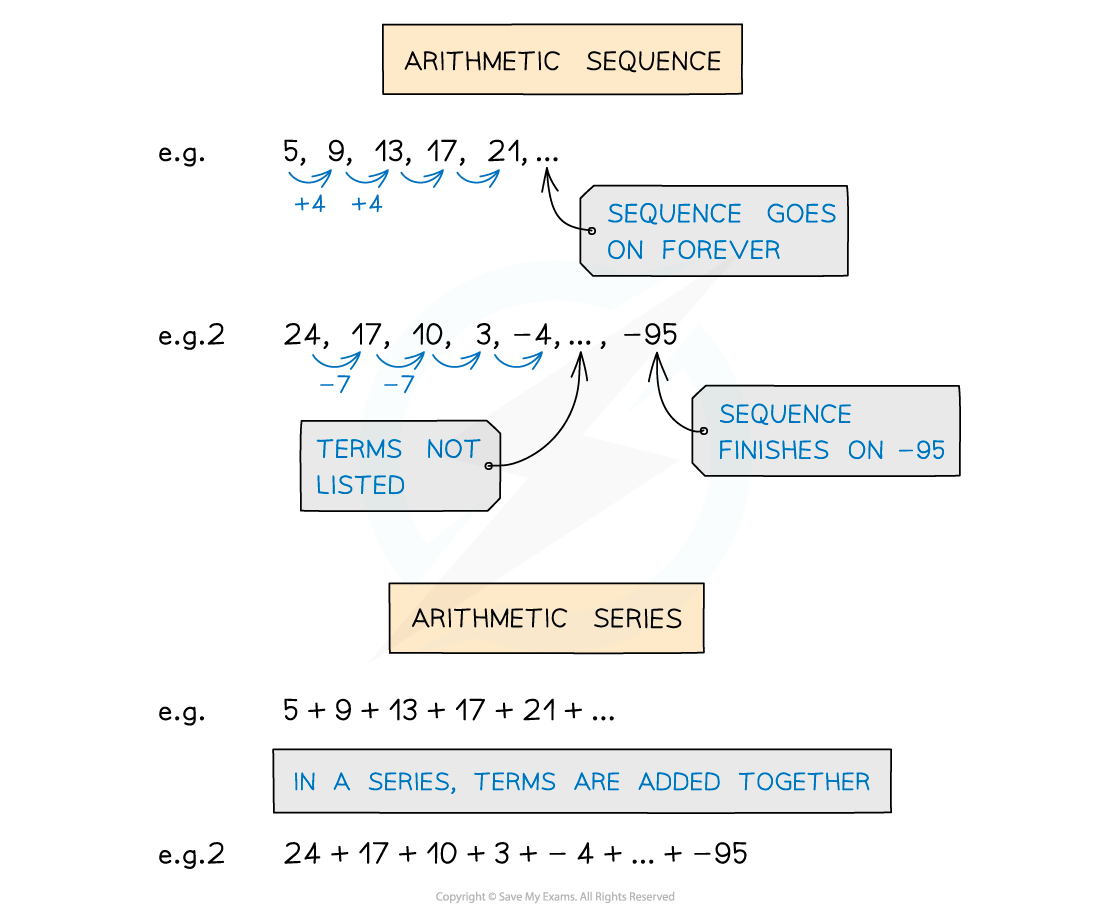
- An arithmetic sequence is a sequence of numbers that increase or decrease by the same amount from one term to the next
- This amount is called the common difference
- eg. 5, 9, 13, 17, 21, ... common difference of 4
- eg2. 24, 17, 10, 3, -4, ..., -95 common difference of -7
- An arithmetic series is where terms are added together
- eg. 5 + 9 + 13 + 17 + 21 + ...
- eg2. 24 + 17 + 10 + 3 + -4 + ... + -95
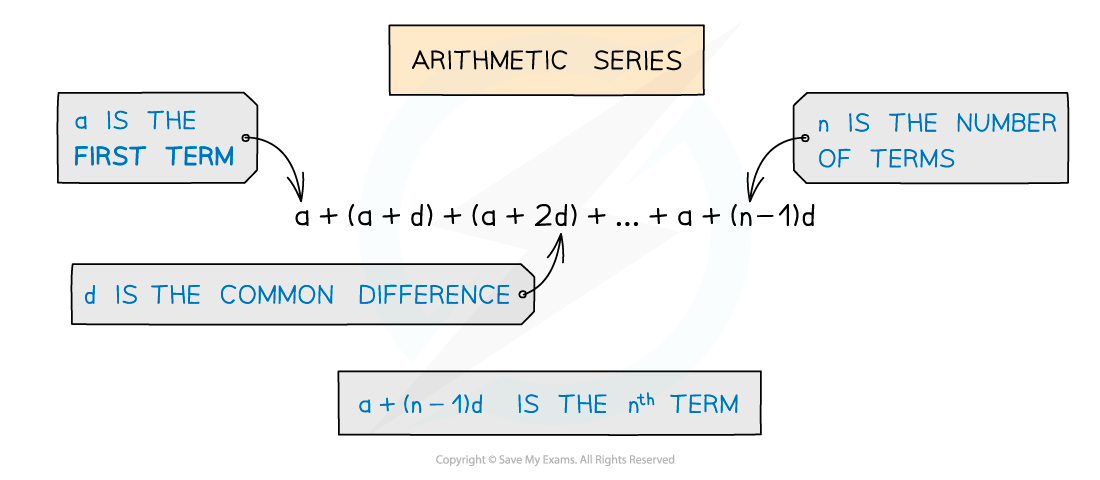
- Lots of letters are used in sequences, make sure you are familiar with them
- a – the first term in an arithmetic series
- d – the common difference of an arithmetic series
- n – the number of terms in the arithmetic seriesSome series go on forever (ie. have an infinite number of terms – but it could be that only the first 10 terms, say, are of interest, so n = 10)
- Sn is used for the sum of the first n terms of an arithmetic series
How do I find the sum of an arithmetic series?
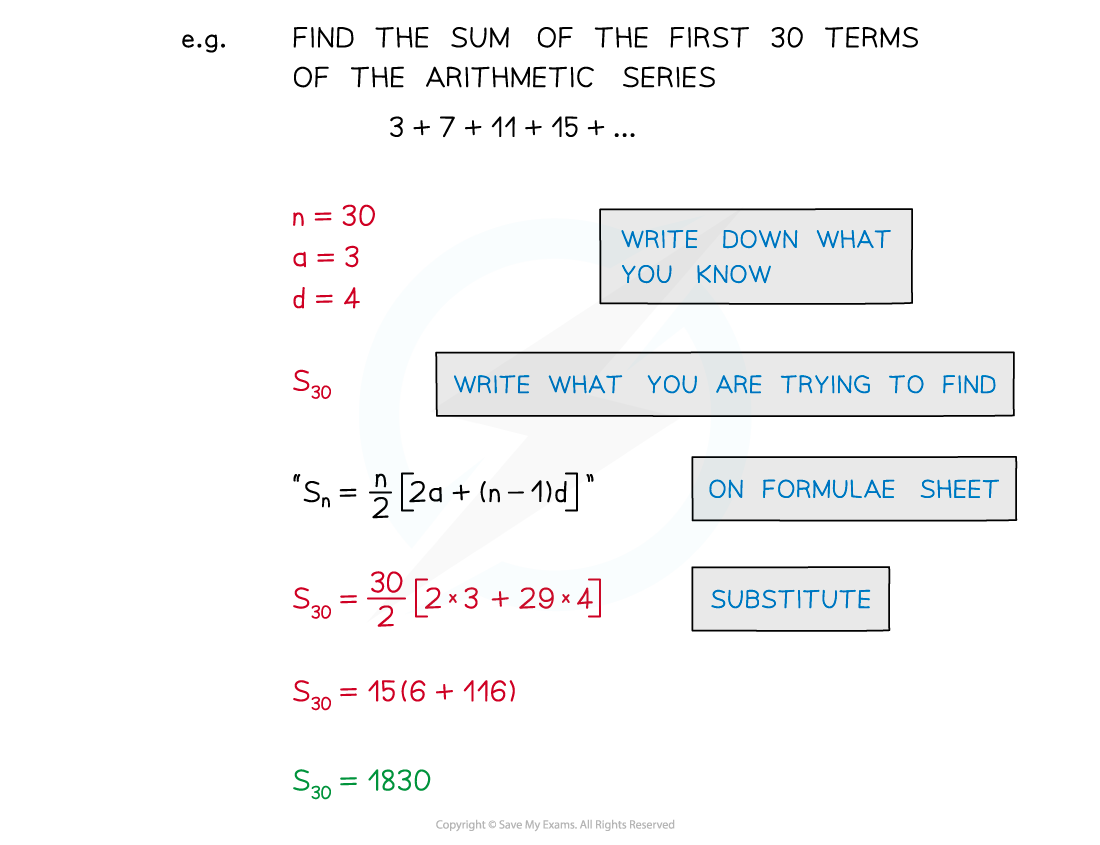
- There is a formula for adding up the first n terms of an arithmetic series
- The formula is included on the formulae sheet
- You do not need to where the formula comes from but, just for fun, here’s a hint
- To add up the numbers 1 to 10
- Write out the numbers1 2 3 4 5 6 7 8 9 10
- Write them backwards10 9 8 7 6 5 4 3 2 1
- Add up both lists11 11 11 11 11 11 11 11 11 11
- This is 10 × 11 = 110
- But this is twice the sum as two lots were added together
- So the sum of the numbers 1 to 10 is 110 ÷ 2 = 55
Exam Tip
It is not necessarily Sn you’ll be asked to find in a question – any of a, d, n and S could be asked for.To avoid confusion always write down what you know and what you are trying to find.Remember that substituting known values into a formula first, then rearranging, is easier than the other way round!
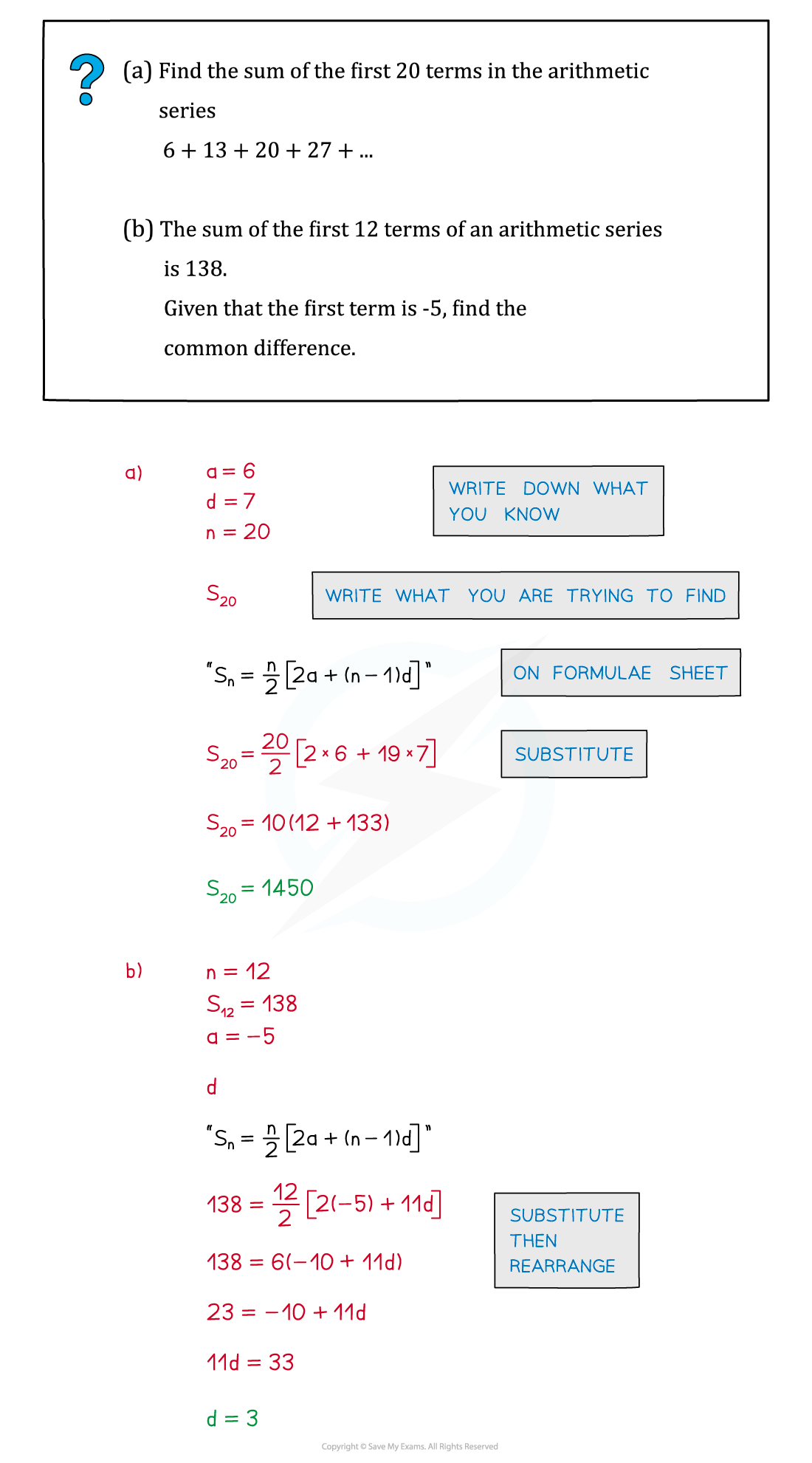
Worked Example
转载自savemyexam
