- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
【同步首发】2018AMC10B官方真题及答案
2018 AMC10B真题
答案解析请参考文末
Problem 1
Kate bakes a 20-inch by 18-inch pan of cornbread. The cornbread is cut into pieces that measure 2 inches by 2 inches. How many pieces of cornbread does the pan contain?
![]()
Problem 2
Sam drove 96 miles in 90 minutes. His average speed during the first 30 minutes was 60 mph (miles per hour), and his average speed during the second 30 minutes was 65 mph. What was his average speed, in mph, during the last 30 minutes?
![]()
Problem 3
In the expression ![]() each blank is to be filled in with one of the digits
each blank is to be filled in with one of the digits ![]() or
or ![]() with each digit being used once. How many different values can be obtained?
with each digit being used once. How many different values can be obtained?
![]()
Problem 4
A three-dimensional rectangular box with dimensions ![]() ,
, ![]() , and
, and ![]() has faces whose surface areas are 24, 24, 48, 48, 72, and 72 square units. What is
has faces whose surface areas are 24, 24, 48, 48, 72, and 72 square units. What is ![]() ?
?
![]()
Problem 5
How many subsets of ![]() contain at least one prime number?
contain at least one prime number?
![]()
Problem 6
A box contains 5 chips, numbered 1, 2, 3, 4, and 5. Chips are drawn randomly one at a time without replacement until the sum of the values drawn exceeds 4. What is the probability that 3 draws are required?
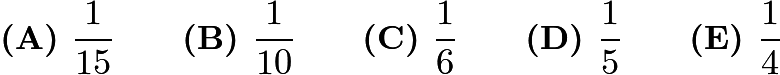
Problem 7
In the figure below, ![]() congruent semicircles are drawn along a diameter of a large semicircle, with their diameters covering the diameter of the large semicircle with no overlap. Let
congruent semicircles are drawn along a diameter of a large semicircle, with their diameters covering the diameter of the large semicircle with no overlap. Let ![]() be the combined area of the small semicircles and
be the combined area of the small semicircles and ![]() be the area of the region inside the large semicircle but outside the small semicircles. The ratio
be the area of the region inside the large semicircle but outside the small semicircles. The ratio ![]() is 1:18. What is
is 1:18. What is ![]() ?
?
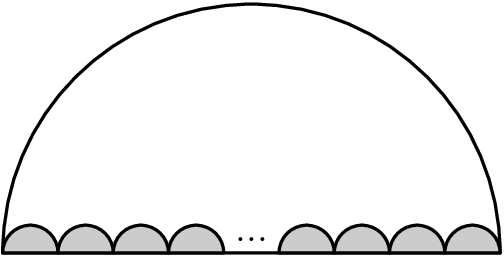
![]()
Problem 8
Sara makes a staircase out of toothpicks as shown:

This is a 3-step staircase and uses 18 toothpicks. How many steps would be in a staircase that used 180 toothpicks?
![]()
Problem 9
The faces of each of 7 standard dice are labeled with the integers from 1 to 6. Let ![]() be the probability that when all 7 dice are rolled, the sum of the numbers on the top faces is 10. What other sum occurs with the same probability
be the probability that when all 7 dice are rolled, the sum of the numbers on the top faces is 10. What other sum occurs with the same probability ![]() ?
?
![]()
Problem 10
In the rectangular parallelepiped shown, ![]() ,
, ![]() , and
, and ![]() . Point
. Point ![]() is the midpoint of
is the midpoint of ![]() . What is the volume of the rectangular pyramid with base
. What is the volume of the rectangular pyramid with base ![]() and apex
and apex ![]() ?
?
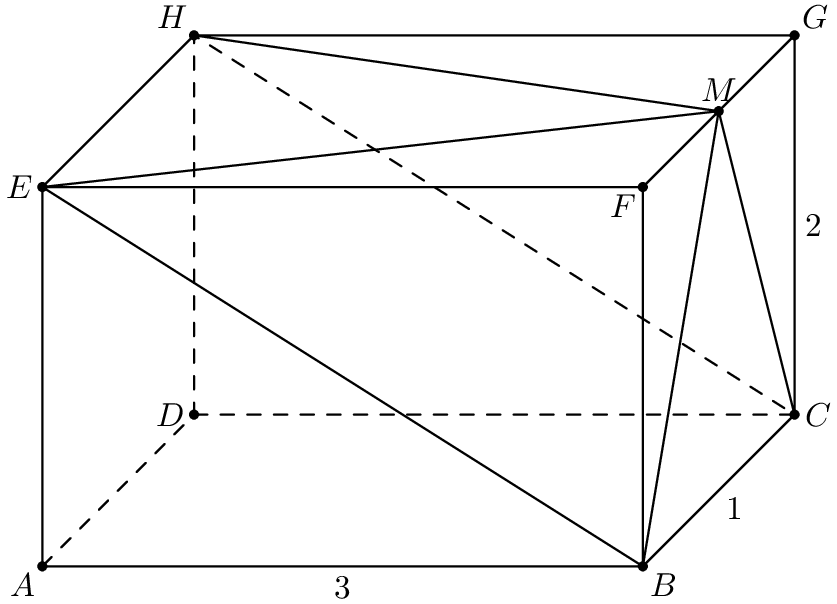
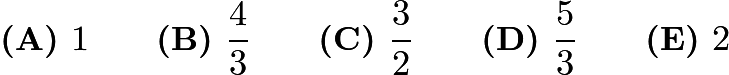
Problem 11
Which of the following expressions is never a prime number when ![]() is a prime number?
is a prime number?
![]()
Problem 12
Line segment ![]() is a diameter of a circle with
is a diameter of a circle with ![]() . Point
. Point ![]() , not equal to
, not equal to ![]() or
or ![]() , lies on the circle. As point
, lies on the circle. As point ![]() moves around the circle, the centroid (center of mass) of
moves around the circle, the centroid (center of mass) of ![]() traces out a closed curve missing two points. To the nearest positive integer, what is the area of the region bounded by this curve?
traces out a closed curve missing two points. To the nearest positive integer, what is the area of the region bounded by this curve?
![]()
Problem 13
How many of the first ![]() numbers in the sequence
numbers in the sequence ![]() are divisible by
are divisible by ![]() ?
?
![]()
Problem 14
A list of ![]() positive integers has a unique mode, which occurs exactly
positive integers has a unique mode, which occurs exactly ![]() times. What is the least number of distinct values that can occur in the list?
times. What is the least number of distinct values that can occur in the list?
![]()
Problem 15
A closed box with a square base is to be wrapped with a square sheet of wrapping paper. The box is centered on the wrapping paper with the vertices of the base lying on the midlines of the square sheet of paper, as shown in the figure on the left. The four corners of the wrapping paper are to be folded up over the sides and brought together to meet at the center of the top of the box, point ![]() in the figure on the right. The box has base length
in the figure on the right. The box has base length ![]() and height
and height ![]() . What is the area of the sheet of wrapping paper?
. What is the area of the sheet of wrapping paper?
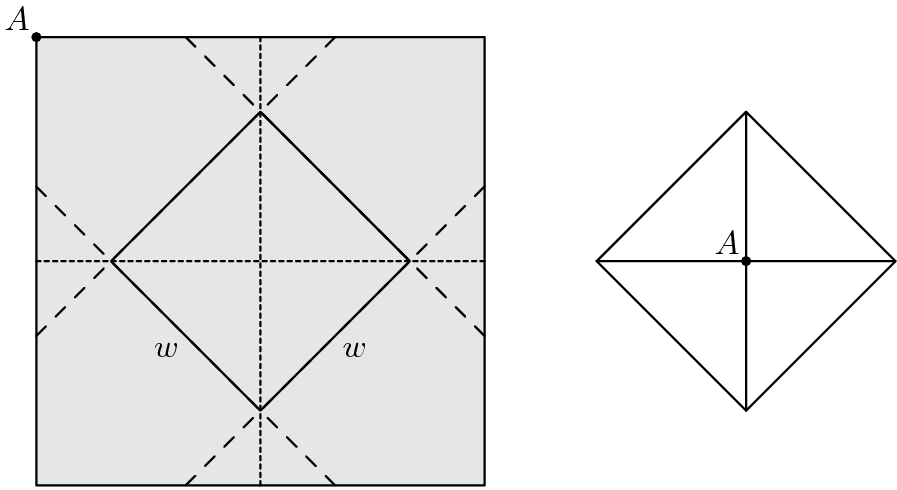
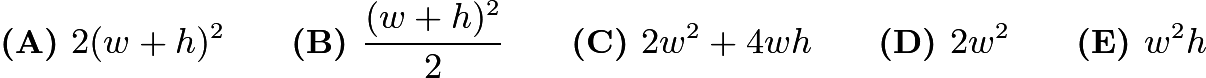
Problem 16
Let ![]() be a strictly increasing sequence of positive integers such that
be a strictly increasing sequence of positive integers such that ![]() What is the remainder when
What is the remainder when ![]() is divided by
is divided by ![]() ?
?
![]()
Problem 17
In rectangle ![]() ,
, ![]() and
and ![]() . Points
. Points ![]() and
and ![]() lie on
lie on ![]() , points
, points ![]() and
and ![]() lie on
lie on ![]() , points
, points ![]() and
and ![]() lie on
lie on ![]() , and points
, and points ![]() and
and ![]() lie on
lie on ![]() so that
so that ![]() and the convex octagon
and the convex octagon ![]() is equilateral. The length of a side of this octagon can be expressed in the form
is equilateral. The length of a side of this octagon can be expressed in the form ![]() , where
, where ![]() ,
, ![]() , and
, and ![]() are integers and
are integers and ![]() is not divisible by the square of any prime. What is
is not divisible by the square of any prime. What is ![]() ?
?
![]()
Problem 18
Three young brother-sister pairs from different families need to take a trip in a van. These six children will occupy the second and third rows in the van, each of which has three seats. To avoid disruptions, siblings may not sit right next to each other in the same row, and no child may sit directly in front of his or her sibling. How many seating arrangements are possible for this trip?
![]()
Problem 19
Joey and Chloe and their daughter Zoe all have the same birthday. Joey is 1 year older than Chloe, and Zoe is exactly 1 year old today. Today is the first of the 9 birthdays on which Chloe's age will be an integral multiple of Zoe's age. What will be the sum of the two digits of Joey's age the next time his age is a multiple of Zoe's age?
![]()
Problem 20
A function ![]() is defined recursively by
is defined recursively by ![]() and
and ![]() for all integers
for all integers ![]() . What is
. What is ![]() ?
?
![]()
Problem 21
Mary chose an even ![]() -digit number
-digit number ![]() . She wrote down all the divisors of
. She wrote down all the divisors of ![]() in increasing order from left to right:
in increasing order from left to right:  . At some moment Mary wrote
. At some moment Mary wrote ![]() as a divisor of
as a divisor of ![]() . What is the smallest possible value of the next divisor written to the right of
. What is the smallest possible value of the next divisor written to the right of ![]() ?
?
![]()
Problem 22
Real numbers ![]() and
and ![]() are chosen independently and uniformly at random from the interval
are chosen independently and uniformly at random from the interval ![]() . Which of the following numbers is closest to the probability that
. Which of the following numbers is closest to the probability that ![]() and
and ![]() are the side lengths of an obtuse triangle?
are the side lengths of an obtuse triangle?
![]()
Problem 23
How many ordered pairs ![]() of positive integers satisfy the equation
of positive integers satisfy the equation ![]() where
where ![]() denotes the greatest common divisor of
denotes the greatest common divisor of ![]() and
and ![]() , and
, and ![]() denotes their least common multiple?
denotes their least common multiple?
![]()
Problem 24
Let ![]() be a regular hexagon with side length
be a regular hexagon with side length ![]() . Denote by
. Denote by ![]() ,
, ![]() , and
, and ![]() the midpoints of sides
the midpoints of sides ![]() ,
, ![]() , and
, and ![]() , respectively. What is the area of the convex hexagon whose interior is the intersection of the interiors of
, respectively. What is the area of the convex hexagon whose interior is the intersection of the interiors of ![]() and
and ![]() ?
?
Problem 25
Let ![]() denote the greatest integer less than or equal to
denote the greatest integer less than or equal to ![]() . How many real numbers
. How many real numbers ![]() satisfy the equation
satisfy the equation ![]() ?
?
![]()
2018AMC10B答案获取方法:翰林国际教育公众号(微信号linstitute)内回复
2018AMC10B
2018 AMC 10B详细解析请注册或登录后查看:
以上解析方式仅供参考
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1









