- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
【同步首发】2018AMC12B官方真题及答案
2018 AMC 12B真题
答案解析请参考文末
Problem 1
Kate bakes 20-inch by 18-inch pan of cornbread. The cornbread is cut into pieces that measure 2 inches by 2 inches. How many pieces of cornbread does the pan contain?
![]()
Problem 2
Sam drove 96 miles in 90 minutes. His average speed during the first 30 minutes was 60 mph (miles per hour), and his average speed during the second 30 minutes was 65 mph. What was his average speed, in mph, during the last 30 minutes?
![]()
Problem 3
A line with slope 2 intersects a line with slope 6 at the point ![]() . What is the distance between the
. What is the distance between the ![]() -intercepts of these two lines?
-intercepts of these two lines?
![]()
Problem 4
A circle has a chord of length ![]() , and the distance from the center of the circle to the chord is
, and the distance from the center of the circle to the chord is ![]() . What is the area of the circle?
. What is the area of the circle?
![]()
Problem 5
How many subsets of ![]() contain at least one prime number?
contain at least one prime number?
![]()
Problem 6
Suppose ![]() cans of soda can be purchased from a vending machine for
cans of soda can be purchased from a vending machine for ![]() quarters. Which of the following expressions describes the number of cans of soda that can be purchased for
quarters. Which of the following expressions describes the number of cans of soda that can be purchased for ![]() dollars, where 1 dollar is worth 4 quarters?
dollars, where 1 dollar is worth 4 quarters?
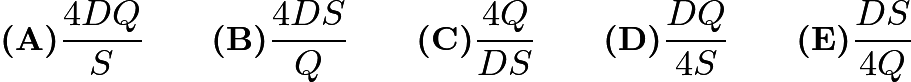
Problem 7
What is the value of![]()
![]()
Problem 8
Line segment ![]() is a diameter of a circle with
is a diameter of a circle with ![]() . Point
. Point ![]() , not equal to
, not equal to ![]() or
or ![]() , lies on the circle. As point
, lies on the circle. As point ![]() moves around the circle, the centroid (center of mass) of
moves around the circle, the centroid (center of mass) of ![]() traces out a closed curve missing two points. To the nearest positive integer, what is the area of the region bounded by this curve?
traces out a closed curve missing two points. To the nearest positive integer, what is the area of the region bounded by this curve?
![]()
Problem 9
What is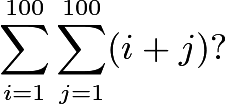
![]()
Problem 10
A list of ![]() positive integers has a unique mode, which occurs exactly
positive integers has a unique mode, which occurs exactly ![]() times. What is the least number of distinct values that can occur in the list?
times. What is the least number of distinct values that can occur in the list?
![]()
Problem 11
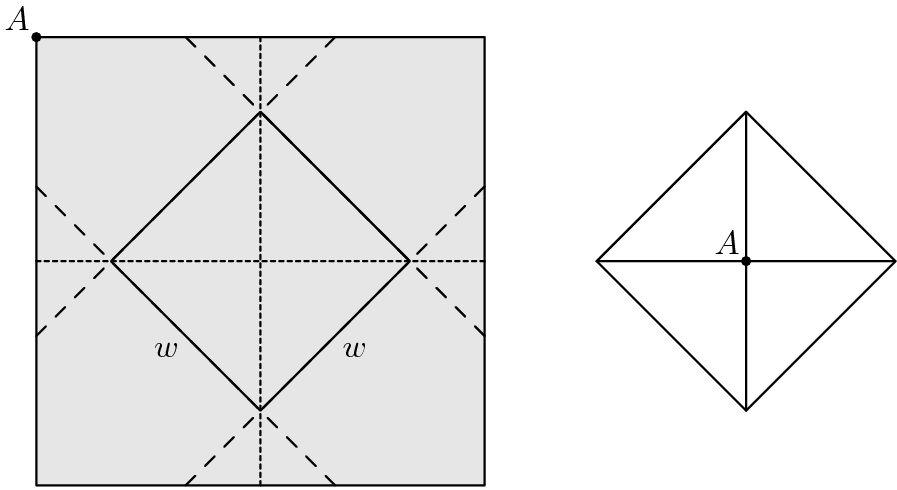
A closed box with a square base is to be wrapped with a square sheet of wrapping paper. The box is centered on the wrapping paper with the vertices of the base lying on the midlines of the square sheet of paper, as shown in the figure on the left. The four corners of the wrapping paper are to be folded up over the sides and brought together to meet at the center of the top of the box, point ![]() in the figure on the right. The box has base length
in the figure on the right. The box has base length ![]() and height
and height ![]() . What is the area of the sheet of wrapping paper?
. What is the area of the sheet of wrapping paper?
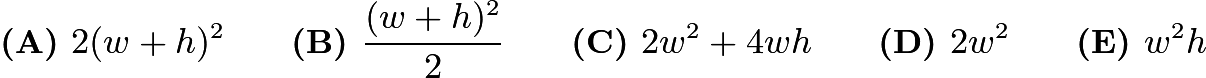
Problem 12
Side ![]() of
of ![]() has length
has length ![]() . The bisector of angle
. The bisector of angle ![]() meets
meets ![]() at
at ![]() , and
, and ![]() . The set of all possible values of
. The set of all possible values of ![]() is an open interval
is an open interval ![]() . What is
. What is ![]() ?
?
![]()
Problem 13
Square ![]() has side length
has side length ![]() . Point
. Point ![]() lies inside the square so that
lies inside the square so that ![]() and
and ![]() . The centroids of
. The centroids of ![]() ,
, ![]() ,
, ![]() , and
, and ![]() are the vertices of a convex quadrilateral. What is the area of that quadrilateral?
are the vertices of a convex quadrilateral. What is the area of that quadrilateral?
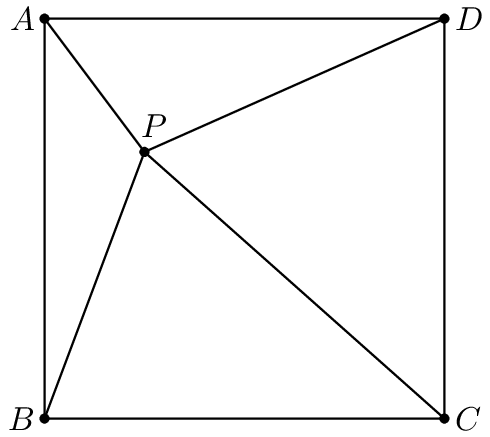
![]()
Problem 14
Joey and Chloe and their daughter Zoe all have the same birthday. Joey is 1 year older than Chloe, and Zoe is exactly 1 year old today. Today is the first of the 9 birthdays on which Chloe's age will be an integral multiple of Zoe's age. What will be the sum of the two digits of Joey's age the next time his age is a multiple of Zoe's age?
![]()
Problem 15
How many odd positive 3-digit integers are divisible by 3 but do not contain the digit 3?
![]()
Problem 16
The solutions to the equation ![]() are connected in the complex plane to form a convex regular polygon, three of whose vertices are labeled
are connected in the complex plane to form a convex regular polygon, three of whose vertices are labeled ![]() and
and ![]() . What is the least possible area of
. What is the least possible area of ![]()
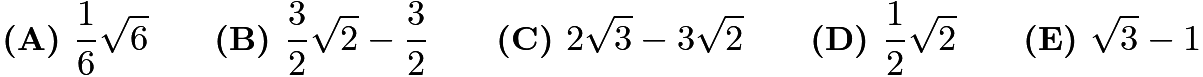
Problem 17
Let ![]() and
and ![]() be positive integers such that
be positive integers such that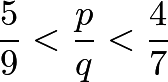 and
and ![]() is as small as possible. What is
is as small as possible. What is ![]() ?
?
![]()
Problem 18
A function ![]() is defined recursively by
is defined recursively by ![]() and
and![]() for all integers
for all integers ![]() . What is
. What is ![]() ?
?
![]()
Problem 19
Mary chose an even ![]() -digit number
-digit number ![]() . She wrote down all the divisors of
. She wrote down all the divisors of ![]() in increasing order from left to right:
in increasing order from left to right:  . At some moment Mary wrote
. At some moment Mary wrote ![]() as a divisor of
as a divisor of ![]() . What is the smallest possible value of the next divisor written to the right of
. What is the smallest possible value of the next divisor written to the right of ![]() ?
?
![]()
Problem 20
Let ![]() be a regular hexagon with side length
be a regular hexagon with side length ![]() . Denote by
. Denote by ![]() ,
, ![]() , and
, and ![]() the midpoints of sides
the midpoints of sides ![]() ,
, ![]() , and
, and ![]() , respectively. What is the area of the convex hexagon whose interior is the intersection of the interiors of
, respectively. What is the area of the convex hexagon whose interior is the intersection of the interiors of ![]() and
and ![]() ?
?
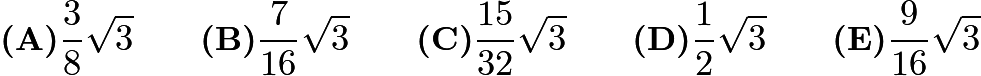
Problem 21
In ![]() with side lengths
with side lengths ![]() ,
, ![]() , and
, and ![]() , let
, let ![]() and
and ![]() denote the circumcenter and incenter, respectively. A circle with center
denote the circumcenter and incenter, respectively. A circle with center ![]() is tangent to the legs
is tangent to the legs ![]() and
and![]() and to the circumcircle of
and to the circumcircle of ![]() . What is the area of
. What is the area of ![]() ?
?
![]()
Problem 22
Consider polynomials ![]() of degree at most
of degree at most ![]() , each of whose coefficients is an element of
, each of whose coefficients is an element of ![]() . How many such polynomials satisfy
. How many such polynomials satisfy ![]() ?
?
![]()
Problem 23
Ajay is standing at point ![]() near Pontianak, Indonesia,
near Pontianak, Indonesia, ![]() latitude and
latitude and ![]() longitude. Billy is standing at point
longitude. Billy is standing at point ![]() near Big Baldy Mountain, Idaho, USA,
near Big Baldy Mountain, Idaho, USA, ![]() latitude and
latitude and ![]() longitude. Assume that Earth is a perfect sphere with center
longitude. Assume that Earth is a perfect sphere with center ![]() . What is the degree measure of
. What is the degree measure of ![]() ?
?
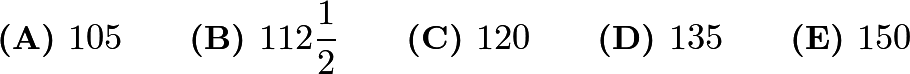
Problem 24
Let ![]() denote the greatest integer less than or equal to
denote the greatest integer less than or equal to ![]() . How many real numbers
. How many real numbers ![]() satisfy the equation
satisfy the equation ![]() ?
?
![]()
Problem 25
Circles ![]() ,
, ![]() , and
, and ![]() each have radius
each have radius ![]() and are placed in the plane so that each circle is externally tangent to the other two. Points
and are placed in the plane so that each circle is externally tangent to the other two. Points ![]() ,
, ![]() , and
, and ![]() lie on
lie on ![]() ,
, ![]() , and
, and ![]() respectively such that
respectively such that ![]() and line
and line ![]() is tangent to
is tangent to ![]() for each
for each ![]() , where
, where ![]() . See the figure below. The area of
. See the figure below. The area of ![]() can be written in the form
can be written in the form ![]() for positive integers
for positive integers ![]() and
and ![]() . What is
. What is ![]() ?
?

![]()
- The area of the pan is
 =
= 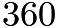 . Since the area of each piece is
. Since the area of each piece is 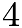 , there are
, there are 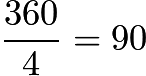 pieces. Thus, the answer is
pieces. Thus, the answer is  .
. - Let Sam drive at exactly
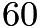 mph in the first half hour,
mph in the first half hour, 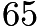 mph in the second half hour, and
mph in the second half hour, and 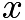 mph in the third half hour.Due to
mph in the third half hour.Due to 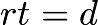 , and that
, and that 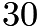 min is half an hour, he covered
min is half an hour, he covered 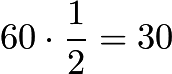 miles in the first
miles in the first 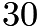 mins.SImilarly, he covered
mins.SImilarly, he covered 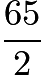 miles in the
miles in the 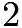 nd half hour period.The problem states that Sam drove
nd half hour period.The problem states that Sam drove 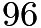 miles in
miles in 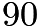 min, so that means that he must have covered
min, so that means that he must have covered 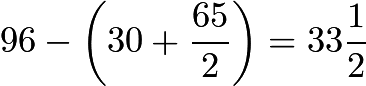 miles in the third half hour period.
miles in the third half hour period. , so
, so 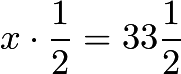 .Therefore, Sam was driving
.Therefore, Sam was driving  miles per hour in the third half hour.
miles per hour in the third half hour. - Using the slope-intercept form, we get the equations
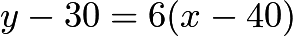 and
and 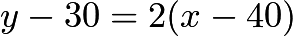 . Simplifying, we get
. Simplifying, we get 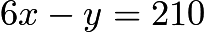 and
and 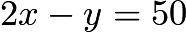 . Letting
. Letting 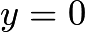 in both equations and solving for
in both equations and solving for 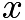 gives the
gives the 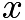 -intercepts:
-intercepts: 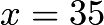 and
and 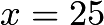 , respectively. Thus the distance between them is
, respectively. Thus the distance between them is 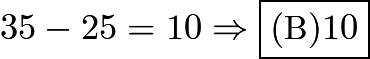
- The shortest segment that connects the center of the circle to a chord is the perpendicular bisector of the chord. Applying the Pythagorean theorem, we find that
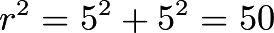 The area of a circle is
The area of a circle is 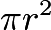 , so the answer is
, so the answer is 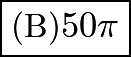
- Since an element of a subset is either in or out, the total number of subsets of the 8 element set is
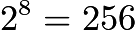 . However, since we are only concerned about the subsets with at least 1 prime in it, we can use complementary counting to count the subsets without a prime and subtract that from the total. Because there are 4 non-primes, there are
. However, since we are only concerned about the subsets with at least 1 prime in it, we can use complementary counting to count the subsets without a prime and subtract that from the total. Because there are 4 non-primes, there are 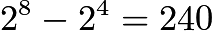 subsets with at least 1 prime so the answer is
subsets with at least 1 prime so the answer is 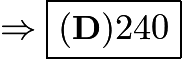
- The unit price for a can of soda (in quarters) is
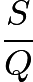 . Thus, the number of cans which can be bought for
. Thus, the number of cans which can be bought for 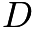 dollars (
dollars (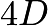 quarters) is
quarters) is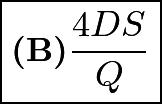
- Change of base makes this
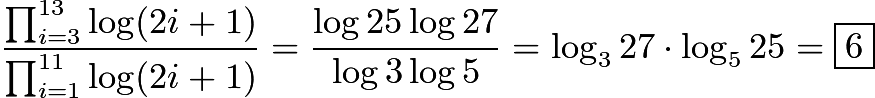
- Draw the Median connecting C to the center O of the circle. Note that the centroid is
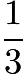 of the distance from O to C. Thus, as C traces a circle of radius 12, the Centroid will trace a circle of radius
of the distance from O to C. Thus, as C traces a circle of radius 12, the Centroid will trace a circle of radius 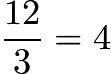 .The area of this circle is
.The area of this circle is 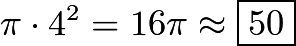 .
. - We can start by writing out the first couple of terms:
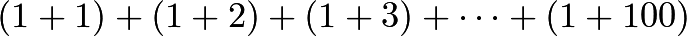
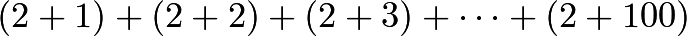
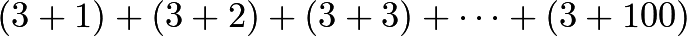

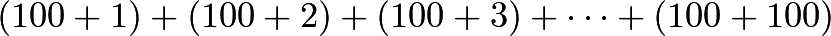 Looking at the second terms in the parentheses, we can see that
Looking at the second terms in the parentheses, we can see that 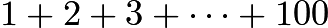 occurs
occurs 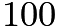 times. It goes horizontally and exists
times. It goes horizontally and exists 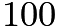 times vertically. Looking at the first terms in the parentheses, we can see that
times vertically. Looking at the first terms in the parentheses, we can see that 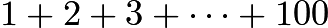 occurs
occurs 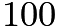 times. It goes vertically and exists
times. It goes vertically and exists 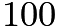 times horizontally.Thus, we have:
times horizontally.Thus, we have: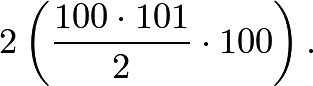 This gives us:
This gives us:
- To minimize the number of values, we want to maximize the number of times they appear. So, we could have 223 numbers appear 9 times, 1 number appear once, and the mode appear 10 times, giving us a total of
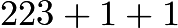 =
= 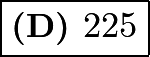
- Consider one-quarter of the image (the wrapping paper is divided up into 4 congruent squares). The length of each dotted line is
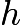 . The area of the rectangle that is
. The area of the rectangle that is 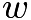 by
by 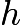 is
is 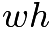 . The combined figure of the two triangles with base
. The combined figure of the two triangles with base 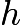 is a square with
is a square with 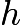 as its diagonal. Using the Pythagorean Theorem, each side of this square is
as its diagonal. Using the Pythagorean Theorem, each side of this square is 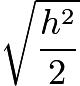 . Thus, the area is the side length squared which is
. Thus, the area is the side length squared which is 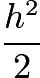 . Similarly, the combined figure of the two triangles with base
. Similarly, the combined figure of the two triangles with base 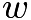 is a square with area
is a square with area 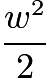 . Adding all of these together, we get
. Adding all of these together, we get 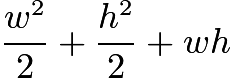 . Since we have four of these areas in the entire wrapping paper, we multiply this by 4, getting
. Since we have four of these areas in the entire wrapping paper, we multiply this by 4, getting 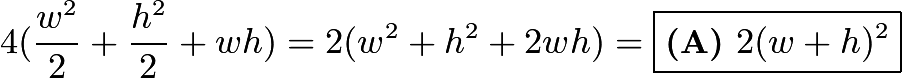 .
. - Let
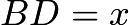 . Then by Angle Bisector Theorem, we have
. Then by Angle Bisector Theorem, we have 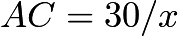 . Now, by the triangle inequality, we have three inequalities.
. Now, by the triangle inequality, we have three inequalities.
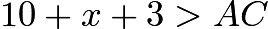 , so
, so 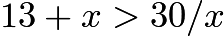 . Solve this to find that
. Solve this to find that 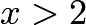 , so
, so  .
.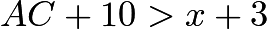 , so
, so 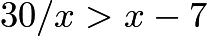 . Solve this to find that
. Solve this to find that  , so
, so 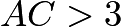 .
.- The third inequality can be disregarded, because
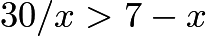 has no real roots.
has no real roots.
Then our interval is simply
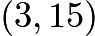 to get
to get 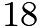
 .
. - We can draw an accurate diagram by using centimeters and scaling everything down by a factor of
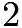 . The centroid is the intersection of the three medians in a triangle.After connecting the
. The centroid is the intersection of the three medians in a triangle.After connecting the 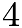 centroids, we see that the quadrilateral looks like a square with side length of
centroids, we see that the quadrilateral looks like a square with side length of 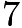 . However, we scaled everything down by a factor of
. However, we scaled everything down by a factor of 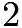 , so the length is
, so the length is 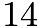 . The area of a square is
. The area of a square is 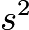 , so the area is:
, so the area is: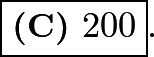
- Let Joey's age be
 , Chloe's age be
, Chloe's age be 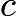 , and we know that Zoe's age is
, and we know that Zoe's age is 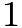 .We know that there must be
.We know that there must be 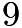 values
values 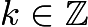 such that
such that 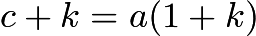 where
where 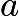 is an integer.Therefore,
is an integer.Therefore, 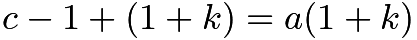 and
and 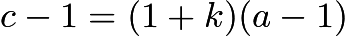 . Therefore, we know that, as there are
. Therefore, we know that, as there are 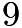 solutions for
solutions for 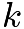 , there must be
, there must be 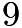 solutions for
solutions for 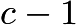 . We know that this must be a perfect square. Testing perfect squares, we see that
. We know that this must be a perfect square. Testing perfect squares, we see that 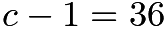 , so
, so 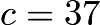 . Therefore,
. Therefore, 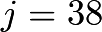 . Now, since
. Now, since 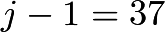 , by similar logic,
, by similar logic, 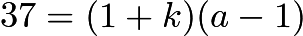 , so
, so 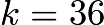 and Joey will be
and Joey will be 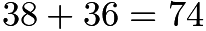 and the sum of the digits is
and the sum of the digits is 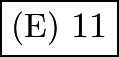
- Analyze that the three-digit integers divisible by
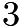 start from
start from 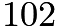 . In the
. In the 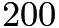 's, it starts from
's, it starts from 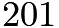 . In the
. In the 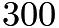 's, it starts from
's, it starts from 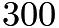 . We see that the units digits is
. We see that the units digits is 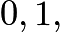 and
and 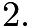 Write out the 1- and 2-digit multiples of
Write out the 1- and 2-digit multiples of 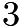 starting from
starting from 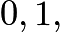 and
and 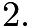 Count up the ones that meet the conditions. Then, add up and multiply by
Count up the ones that meet the conditions. Then, add up and multiply by 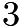 , since there are three sets of three from
, since there are three sets of three from 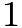 to
to 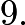 Then, subtract the amount that started from
Then, subtract the amount that started from  , since the
, since the 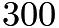 's all contain the digit
's all contain the digit 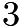 .We get:
.We get: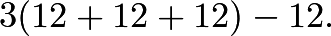 This gives us:
This gives us: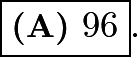
- The answer is the same if we consider
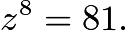 Now we just need to find the area of the triangle bounded by
Now we just need to find the area of the triangle bounded by 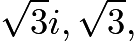 and
and 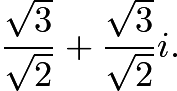 This is just
This is just 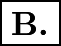
- We claim that, between any two fractions
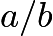 and
and 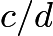 , if
, if 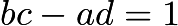 , the fraction with smallest denominator between them is
, the fraction with smallest denominator between them is 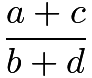 . To prove this, we see that
. To prove this, we see that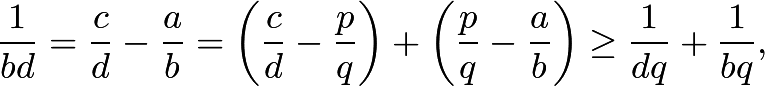 which reduces to
which reduces to 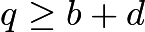 . We can easily find that
. We can easily find that 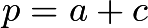 , giving an answer of
, giving an answer of  .
. 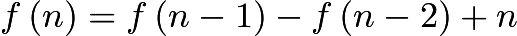
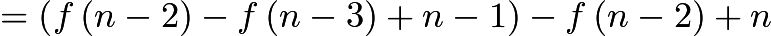
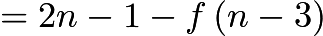
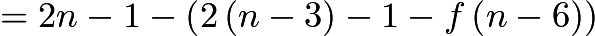
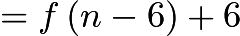 Thus,
Thus, 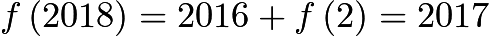 .
. 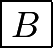
- Prime factorizing
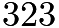 gives you
gives you  . The desired answer needs to be a multiple of
. The desired answer needs to be a multiple of 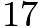 or
or 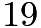 , because if it is not a multiple of
, because if it is not a multiple of 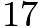 or
or 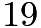 , the LCM, or the least possible value for
, the LCM, or the least possible value for 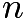 , will not be more than 4 digits. Looking at the answer choices,
, will not be more than 4 digits. Looking at the answer choices, 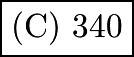 is the smallest number divisible by
is the smallest number divisible by 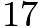 or
or 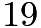 . Checking, we can see that
. Checking, we can see that 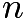 would be
would be 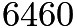 .
. 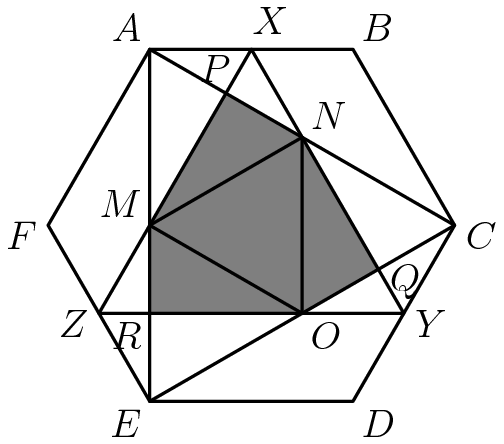 The desired area (hexagon
The desired area (hexagon  ) consists of an equilateral triangle (
) consists of an equilateral triangle ( ) and three right triangles (
) and three right triangles ( ,
, 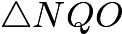 , and
, and 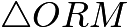 ).Notice that
).Notice that 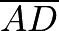 (not shown) and
(not shown) and 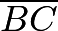 are parallel.
are parallel. 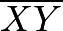 divides transversals
divides transversals 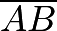 and
and 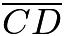 into a
into a  ratio. Thus, it must also divide transversal
ratio. Thus, it must also divide transversal 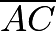 and transversal
and transversal 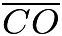 into a
into a  ratio. By symmetry, the same applies for
ratio. By symmetry, the same applies for  and
and 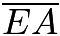 as well as
as well as 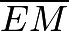 and
and 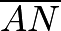 In
In 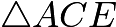 , we see that
, we see that 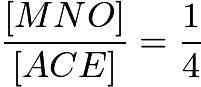 and
and 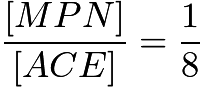 . Our desired area becomes
. Our desired area becomes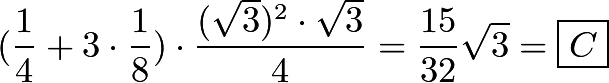
- Let the triangle have coordinates
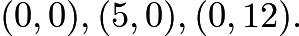 Then the coordinates of the incenter and circumcenter are
Then the coordinates of the incenter and circumcenter are 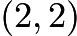 and
and 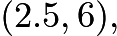 respectively. If we let
respectively. If we let 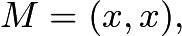 then
then 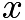 satisfies
satisfies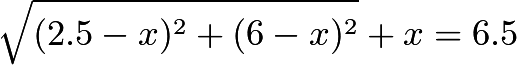
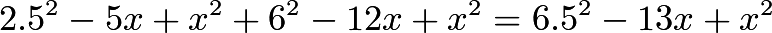
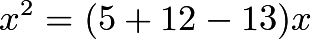
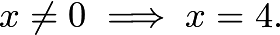 Now the area of our triangle can be calculated with the Shoelace Theorem. The answer turns out to be
Now the area of our triangle can be calculated with the Shoelace Theorem. The answer turns out to be 
- Suppose our polynomial is equal to
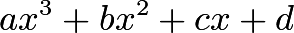 Then we are given that
Then we are given that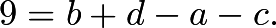 If we let
If we let 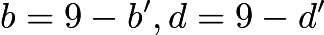 then we have
then we have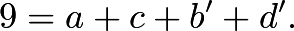 The number of solutions to this equation is simply
The number of solutions to this equation is simply 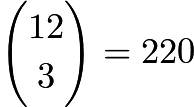 by stars and bars, so our answer is
by stars and bars, so our answer is 
- Suppose that Earth is a unit sphere with center
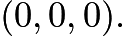 We can let
We can let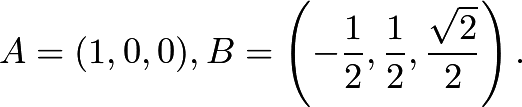 The angle
The angle 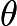 between these two vectors satisfies
between these two vectors satisfies 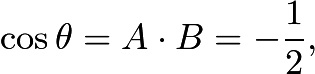 yielding
yielding 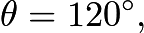 or
or 
- This rewrites itself to
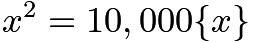 .Graphing
.Graphing 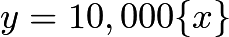 and
and 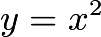 we see that the former is a set of line segments with slope
we see that the former is a set of line segments with slope 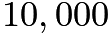 from
from  to
to 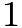 with a hole at
with a hole at 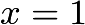 , then
, then 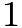 to
to 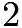 with a hole at
with a hole at 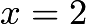 etc.Here is a graph of
etc.Here is a graph of 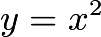 and
and 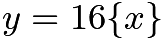 for visualization.
for visualization.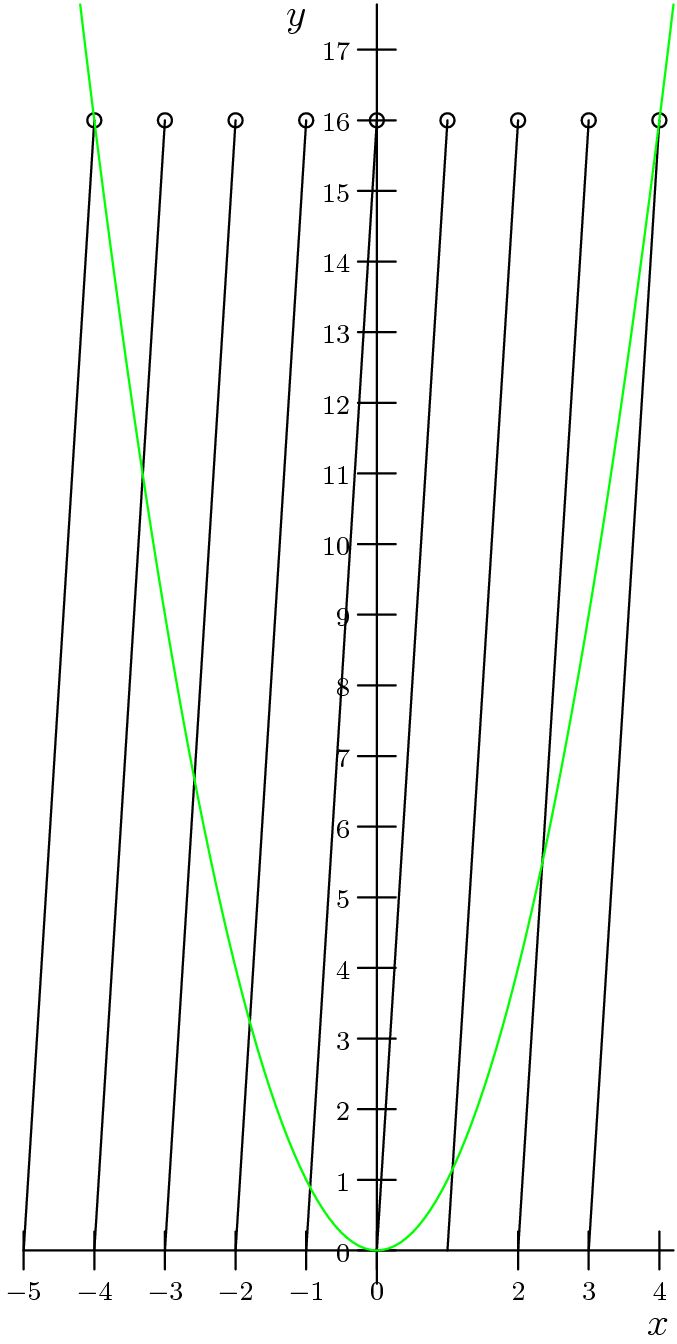 Now notice that when
Now notice that when 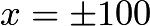 then graph has a hole at
then graph has a hole at 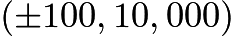 which the equation
which the equation 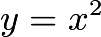 passes through and then continues upwards. Thus our set of possible solutions is bounded by
passes through and then continues upwards. Thus our set of possible solutions is bounded by 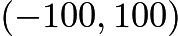 . We can see that
. We can see that 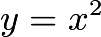 intersects each of the lines once and there are
intersects each of the lines once and there are 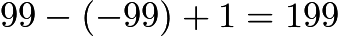 lines for an answer of
lines for an answer of  .
. - Let
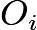 be the center of circle
be the center of circle 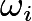 for
for 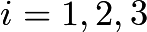 , and let
, and let 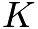 be the intersection of lines
be the intersection of lines 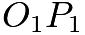 and
and 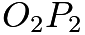 . Because
. Because 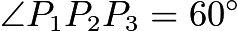 , it follows that
, it follows that 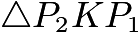 is a
is a 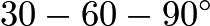 triangle. Let
triangle. Let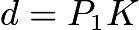 ; then
; then 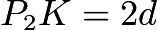 and
and 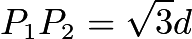 . The Law of Cosines in
. The Law of Cosines in 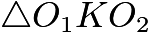 gives
gives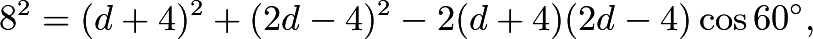 which simplifies to
which simplifies to 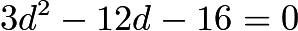 . The positive solution is
. The positive solution is 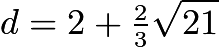 . Then
. Then 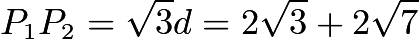 , and the required area is
, and the required area is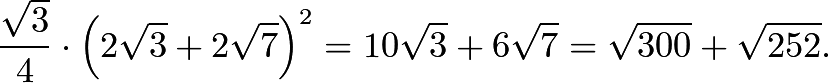 The requested sum is
The requested sum is 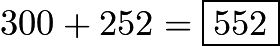 .
.
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





