- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
全球顶尖数学夏校——罗斯数学训练营(Ross)正式开放申请!申请流程+入营测试
众所周知,对于想通过学术亮点进入前20名校的学生来说,能申请到一个非常具有含金量的项目,论证自己的学术能力非常重要,几乎可以说“一只脚已经踏入了藤校”。近日,美国顶尖数学夏令营——Ross数学营正式开始招募!
经历2020-2021疫情影响之后,美国顶尖数学夏令营——Ross数学营决定2022年取消线上营以及亚洲营地,转而在美国开设两个线下营地,每个营地招收60名新生。夏校课程大多都是以美国学校为基地,由本校的老师上课,拥有成熟固定的课程供大家选择,涉及的内容包括ESL、科学、体育、艺术等等。
夏校之中分的种类也很多,首先是一切学科的基础——数学夏校。
申请数学夏校的好处如下:
数学是理化生及经济学的基础学科,对于不确定未来专业方向的学生来讲申请数学夏校是最稳妥最有效的背景提升方法;
ROSS、SUMaC、PROMYS等顶尖数学夏校含金量极高,录取的国际学生少之又少,进入这些数学夏校意味着一条腿已经踏进了常青藤;
数学夏校一般不强制要求标化成绩,对于数学优异却没有时间刷标化的同学们来讲,更人性化。
罗斯数学训练营The Ross Mathematics Program
项目课程
创办时间:1957年
资方:圣母大学教授创办、俄亥俄州立大学主办、克雷数学研究所协办
参与年级:15-18岁
项目所在地:分为美国营和亚洲营(2016年第一届),美国营1964-2018举办地为俄亥俄州立大学,2019为俄亥俄多米尼加大学,2020-2021为线上项目
费用:$1500(2021年)
项目特点
和众多美国大学为高中生开设的学分夏校(2-6周时长)不同,Ross不提供大学课程学分,也不计算课程成绩和GPA。所有完成项目的学生,将会在项目结束时收到官方颁发的结业证书,表现优异的学生提供教授推荐信。
每周上课时间少。除了每周固定的5小时讲座和3小时研讨会,其余时间学生均用来完成课上未解决的数学题,学生可选择独立完成题目或和助教、同学讨论。在解决每一个数学题后,学生必须提交一份清晰、完整的英文证明过程,锻炼逻辑思维和撰写严谨数学证明的能力。
Ross课程将会加深学生对数论 (Number Theory) 的理解和运用,为大学本科甚至研究生阶段的数学学习打下坚实基础。通过完成每个课程主题的数学题,学生将熟练掌握数论证明的过程:总结规律、提出假设、探索能证明假设的例子、总结数论、撰写数论证明、完善数论、并探索数论的具体应用。
“简单问题,深度思考”是罗斯训练营的主要理念。
美国及其他世界名校数学教授倾情授课,课外辅导与讨论相结合,通过具体的数论问题研究,旨在激发学员对数学学习的兴趣,培养辩证思维能力。
营期全封闭管理学习,为数学爱好者提供难得的学习交流平台。
具体的课程科目有:欧几里得算法、模运算、二项式系数、多项式、元素的阶、二次互反性、连分式、算术函数、高斯整数、有限域等。
申请材料
01必须提交
官网数学题解答 (一共4题,每题以手写或LaTeX格式作答,需详细描述解题思路和论证过程,以PDF格式提交)
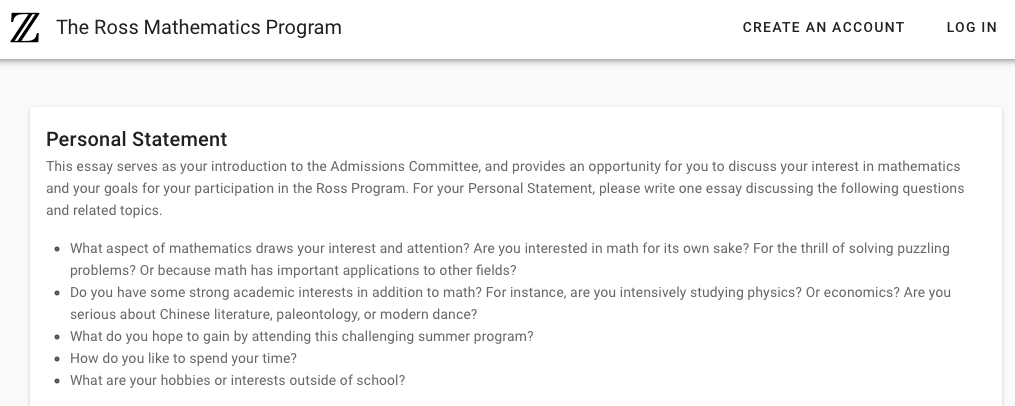
1篇个人陈述(字数不限),阐述学生对数学的兴趣、成就和申请项目的原因
8篇简短回答(字数不限), 可参考:https://apply.rossprogram.org/apply/essays
高中官方成绩单
1篇高中数学老师推荐信
英语能力证明(如托福、雅思成绩)
02选择提交
奖学金申请
简历(以强调数学方面的成就为主)
数学相关学术活动奖项
以下为Ross官网发布的2021年文书题目
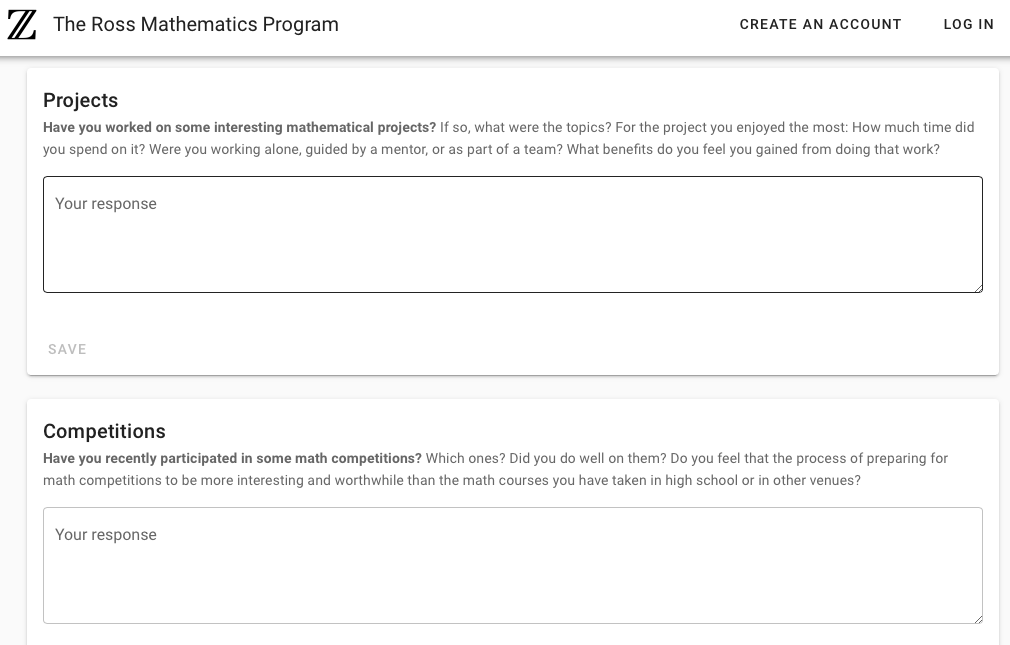
以下为Ross官网发布的2021年数学题

2022Ross夏校申请题
Ross营申请材料中,申请题Solution是必须要提交的一项材料,随着申请通道的开放,今年的入营试题也已经公布了↓
※申请题目一览
The number systems Z and Zm (for a positive integer m) were defined in the previous
problem. We also use the notations:
Q is the system of rational numbers.
4Z is the set of multiples of 4 in Z. Similarly for 4Z12.
Consider the following number systems:
Z, Q, 4Z, Z3, Z8, Z9, 4Z12, Z13.
One system may be viewed as similar to another in several different ways.
(a) Let’s measure similarity using algebraic properties. First consider the following
sample properties:
(i) If a2 = 1, then a = ±1.
(ii) If 2x = 0, then x = 0.
(iii) If c2 = 0, then c = 0.
Which of the systems above have properties (i), (ii), and/or (iii)?
(b) Formulate another algebraic property and determine which of those systems have
that property.
Write down some additional algebraic properties and investigate them.
(c) In your opinion, which of the listed systems are “most similar” to each another?
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





