- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
2020 AIME I真题及答案 高清文字版
2020 AIME I真题及答案
参考答案见文末(仅供参考)
Problem 1
In ![]() with
with ![]() point
point ![]() lies strictly between
lies strictly between ![]() and
and ![]() on side
on side ![]() and point
and point ![]() lies strictly between
lies strictly between ![]() and
and ![]() on side
on side ![]() such that
such that ![]() The degree measure of
The degree measure of ![]() is
is ![]() where
where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]()
Problem 2
There is a unique positive real number ![]() such that the three numbers
such that the three numbers ![]() ,
, ![]() , and
, and ![]() , in that order, form a geometric progression with positive common ratio. The number
, in that order, form a geometric progression with positive common ratio. The number ![]() can be written as
can be written as ![]() , where
, where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]() .
.
Problem 3
A positive integer ![]() has base-eleven representation
has base-eleven representation ![]() and base-eight representation
and base-eight representation ![]() where
where ![]() and
and ![]() represent (not necessarily distinct) digits. Find the least such
represent (not necessarily distinct) digits. Find the least such ![]() expressed in base ten.
expressed in base ten.
Problem 4
Let ![]() be the set of positive integers
be the set of positive integers ![]() with the property that the last four digits of
with the property that the last four digits of ![]() are
are ![]() and when the last four digits are removed, the result is a divisor of
and when the last four digits are removed, the result is a divisor of ![]() For example,
For example, ![]() is in
is in ![]() because
because ![]() is a divisor of
is a divisor of ![]() Find the sum of all the digits of all the numbers in
Find the sum of all the digits of all the numbers in ![]() For example, the number
For example, the number ![]() contributes
contributes ![]() to this total.
to this total.
Problem 5
Six cards numbered ![]() through
through ![]() are to be lined up in a row. Find the number of arrangements of these six cards where one of the cards can be removed leaving the remaining five cards in either ascending or descending order.
are to be lined up in a row. Find the number of arrangements of these six cards where one of the cards can be removed leaving the remaining five cards in either ascending or descending order.
Problem 6
A flat board has a circular hole with radius ![]() and a circular hole with radius
and a circular hole with radius ![]() such that the distance between the centers of the two holes is
such that the distance between the centers of the two holes is ![]() Two spheres with equal radii sit in the two holes such that the spheres are tangent to each other. The square of the radius of the spheres is
Two spheres with equal radii sit in the two holes such that the spheres are tangent to each other. The square of the radius of the spheres is ![]() where
where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]()
Problem 7
A club consisting of ![]() men and
men and ![]() women needs to choose a committee from among its members so that the number of women on the committee is one more than the number of men on the committee. The committee could have as few as
women needs to choose a committee from among its members so that the number of women on the committee is one more than the number of men on the committee. The committee could have as few as ![]() member or as many as
member or as many as ![]() members. Let
members. Let ![]() be the number of such committees that can be formed. Find the sum of the prime numbers that divide
be the number of such committees that can be formed. Find the sum of the prime numbers that divide ![]()
Problem 8
A bug walks all day and sleeps all night. On the first day, it starts at point ![]() faces east, and walks a distance of
faces east, and walks a distance of ![]() units due east. Each night the bug rotates
units due east. Each night the bug rotates ![]() counterclockwise. Each day it walks in this new direction half as far as it walked the previous day. The bug gets arbitrarily close to the point
counterclockwise. Each day it walks in this new direction half as far as it walked the previous day. The bug gets arbitrarily close to the point ![]() Then
Then ![]() where
where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]()
Problem 9
Let ![]() be the set of positive integer divisors of
be the set of positive integer divisors of ![]() Three numbers are chosen independently and at random with replacement from the set
Three numbers are chosen independently and at random with replacement from the set ![]() and labeled
and labeled ![]() and
and ![]() in the order they are chosen. The probability that both
in the order they are chosen. The probability that both ![]() divides
divides ![]() and
and ![]() divides
divides ![]() is
is ![]() where
where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]()
Problem 10
Let ![]() and
and ![]() be positive integers satisfying the conditions
be positive integers satisfying the conditions
![]()
![]() is a multiple of
is a multiple of ![]() and
and
![]() is not a multiple of
is not a multiple of ![]()
Find the least possible value of ![]()
Problem 11
For integers ![]() and
and ![]() let
let ![]() and
and ![]() Find the number of ordered triples
Find the number of ordered triples ![]() of integers with absolute values not exceeding
of integers with absolute values not exceeding ![]() for which there is an integer
for which there is an integer ![]() such that
such that ![]()
Problem 12
Let ![]() be the least positive integer for which
be the least positive integer for which ![]() is divisible by
is divisible by ![]() Find the number of positive integer divisors of
Find the number of positive integer divisors of ![]()
Problem 13
Point ![]() lies on side
lies on side ![]() of
of ![]() so that
so that ![]() bisects
bisects ![]() The perpendicular bisector of
The perpendicular bisector of ![]() intersects the bisectors of
intersects the bisectors of ![]() and
and ![]() in points
in points ![]() and
and ![]() respectively. Given that
respectively. Given that ![]() and
and ![]() the area of
the area of ![]() can be written as
can be written as ![]() where
where ![]() and
and ![]() are relatively prime positive integers, and
are relatively prime positive integers, and ![]() is a positive integer not divisible by the square of any prime. Find
is a positive integer not divisible by the square of any prime. Find ![]()
Problem 14
Let ![]() be a quadratic polynomial with complex coefficients whose
be a quadratic polynomial with complex coefficients whose ![]() coefficient is
coefficient is ![]() Suppose the equation
Suppose the equation ![]() has four distinct solutions,
has four distinct solutions, ![]() Find the sum of all possible values of
Find the sum of all possible values of ![]()
Problem 15
Let ![]() be an acute triangle with circumcircle
be an acute triangle with circumcircle ![]() and let
and let ![]() be the intersection of the altitudes of
be the intersection of the altitudes of ![]() Suppose the tangent to the circumcircle of
Suppose the tangent to the circumcircle of ![]() at
at ![]() intersects
intersects ![]() at points
at points ![]() and
and ![]() with
with ![]() and
and ![]() The area of
The area of ![]() can be written as
can be written as ![]() where
where ![]() and
and ![]() are positive integers, and
are positive integers, and ![]() is not divisible by the square of any prime. Find
is not divisible by the square of any prime. Find ![]()
- Solution 1
![[asy] size(10cm); pair A, B, C, D, F; A = (0, tan(3 * pi / 7)); B = (1, 0); C = (-1, 0); F = rotate(90/7, A) * (A - (0, 2)); D = rotate(900/7, F) * A; draw(A -- B -- C -- cycle); draw(F -- D); draw(D -- B); label("$A$", A, N); label("$B$", B, E); label("$C$", C, W); label("$D$", D, W); label("$E$", F, E); [/asy]](https://latex.artofproblemsolving.com/e/9/e/e9e27ce12b66c38e61f3aeeeec6ac0760eebc7e9.png)
If we set ![]() to
to ![]() , we can find all other angles through these two properties: 1. Angles in a triangle sum to
, we can find all other angles through these two properties: 1. Angles in a triangle sum to ![]() . 2. The base angles of an isosceles triangle are congruent.
. 2. The base angles of an isosceles triangle are congruent.
Now we angle chase. ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Since
. Since ![]() as given by the problem,
as given by the problem, ![]() , so
, so ![]() . Therefore,
. Therefore, ![]() , and our desired angle is
, and our desired angle is![]() for an answer of
for an answer of ![]() .
.
Solution 2
Let ![]() be
be ![]() in degrees.
in degrees. ![]() . By Exterior Angle Theorem on triangle
. By Exterior Angle Theorem on triangle ![]() ,
, ![]() . By Exterior Angle Theorem on triangle
. By Exterior Angle Theorem on triangle ![]() ,
, ![]() . This tells us
. This tells us ![]() and
and ![]() . Thus
. Thus ![]() and we want
and we want ![]() to get an answer of
to get an answer of ![]() .
.
Solution 3 (Official MAA)
Let ![]() . Because
. Because ![]() is isosceles,
is isosceles, ![]() . Then
. Then![]() Because
Because ![]() and
and ![]() are also isosceles,
are also isosceles,![]()
![]() Because
Because ![]() is isosceles,
is isosceles, ![]() is also
is also ![]() , so
, so ![]() , and it follows that
, and it follows that ![]() . The requested sum is
. The requested sum is ![]() .
.
![[asy] unitsize(4 cm); pair A, B, C, D, E; real a = 180/7; A = (0,0); B = dir(180 - a/2); C = dir(180 + a/2); D = extension(B, B + dir(270 + a), A, C); E = extension(D, D + dir(90 - 2*a), A, B); draw(A--B--C--cycle); draw(B--D--E); label("$A$", A, dir(0)); label("$B$", B, NW); label("$C$", C, SW); label("$D$", D, S); label("$E$", E, N); [/asy]](https://latex.artofproblemsolving.com/8/0/0/800a1b87e83f02303a544a1cc3b37b3a774d9483.png)
2.Solution1
Since these form a geometric series, ![]() is the common ratio. Rewriting this, we get
is the common ratio. Rewriting this, we get ![]() by base change formula. Therefore, the common ratio is 2. Now
by base change formula. Therefore, the common ratio is 2. Now ![]()
![]() . Therefore,
. Therefore, ![]() .
.
Solution 2
If we set ![]() , we can obtain three terms of a geometric sequence through logarithm properties. The three terms are
, we can obtain three terms of a geometric sequence through logarithm properties. The three terms are![]() In a three-term geometric sequence, the middle term squared is equal to the product of the other two terms, so we obtain the following:
In a three-term geometric sequence, the middle term squared is equal to the product of the other two terms, so we obtain the following:![]() which can be solved to reveal
which can be solved to reveal ![]() . Therefore,
. Therefore, ![]() , so our answer is
, so our answer is ![]() .
.
Solution 3
Let ![]() be the common ratio. We have
be the common ratio. We have![]() Hence we obtain
Hence we obtain![]() Ideally we change everything to base
Ideally we change everything to base ![]() and we can get:
and we can get:![]() Now divide to get:
Now divide to get:![]() By change-of-base we obtain:
By change-of-base we obtain:![]() Hence
Hence ![]() and we have
and we have ![]() as desired.
as desired.
~skyscraper
Solution 4 (Exponents > Logarithms)
Let ![]() be the common ratio, and let
be the common ratio, and let ![]() be the starting term (
be the starting term (![]() ). We then have:
). We then have:![]() Rearranging these equations gives:
Rearranging these equations gives:![]() Deal with the last two equations first: Setting them equal gives:
Deal with the last two equations first: Setting them equal gives:![]() Using LTE results in:
Using LTE results in:![]() Using this value of
Using this value of ![]() , substitute into the first and second equations (or the first and third, it doesn't really matter) to get:
, substitute into the first and second equations (or the first and third, it doesn't really matter) to get:![]() Changing these to a common base gives:
Changing these to a common base gives:![]() Dividing the first equation by 2 on both sides yields:
Dividing the first equation by 2 on both sides yields:![]() Setting these equations equal to each other and applying LTE again gives:
Setting these equations equal to each other and applying LTE again gives:![]() Substituting this back into the first equation gives:
Substituting this back into the first equation gives:![]() Therefore,
Therefore, ![]()
~IAmTheHazard
Solution 5
We can relate the logarithms as follows:
![]()
![]()
Now we can convert all logarithm bases to ![]() using the identity
using the identity ![]() :
:
![]()
We can solve for ![]() as follows:
as follows:
![]()
![]()
![]() We get
We get ![]() . Verifying that the common ratio is positive, we find the answer of
. Verifying that the common ratio is positive, we find the answer of ![]() .
.
~QIDb602
Solution 6
If the numbers are in a geometric sequence, the middle term must be the geometric mean of the surrounding terms. We can rewrite the first two logarithmic expressions as ![]() and
and ![]() , respectively. Therefore:
, respectively. Therefore:![\[\frac{1}{2}\log_2{x}=\sqrt{\left(\frac{1+\log_2{x}}{3}\right)\left(\log_2{x}\right)}\]](https://latex.artofproblemsolving.com/8/6/3/863ae271c3e4b2a145ad891f77281a6dc81ef154.png) Let
Let ![]() . We can rewrite the expression as:
. We can rewrite the expression as:![]()
![]()
![]()
![]()
![]()
![]()
![]() Zero does not work in this case, so we consider
Zero does not work in this case, so we consider ![]() :
: ![]() . Therefore,
. Therefore, ![]() .
.
~Bowser498
Solution 7 (Official MAA)
By the Change of Base Formula the common ratio of the progression is![]() Hence
Hence ![]() must satisfy
must satisfy![]() This is equivalent to
This is equivalent to ![]() . Hence
. Hence ![]() and
and ![]() . The requested sum is
. The requested sum is ![]() .
.
3.Solution 1
From the given information, ![]() . Since
. Since ![]() ,
, ![]() , and
, and ![]() have to be positive,
have to be positive, ![]() . Since we need to minimize the value of
. Since we need to minimize the value of ![]() , we want to minimize
, we want to minimize ![]() , so we have
, so we have ![]() . Then we know
. Then we know ![]() , and we can see the only solution is
, and we can see the only solution is ![]() ,
, ![]() . Finally,
. Finally, ![]() , so our answer is
, so our answer is ![]() .
.
~ JHawk0224
Solution 2 (Official MAA)
The conditions of the problem imply that ![]() , so
, so ![]() . The maximum digit in base eight is
. The maximum digit in base eight is ![]() and because
and because ![]() , it must be that
, it must be that ![]() is
is ![]() or
or ![]() When
When ![]() , it follows that
, it follows that ![]() , which implies that
, which implies that ![]() . Then
. Then ![]() must be
must be ![]() or
or ![]() If
If ![]() , then
, then ![]() is not an integer, and if
is not an integer, and if ![]() , then
, then ![]() , so
, so ![]() . Thus
. Thus ![]() , and
, and ![]() . The number
. The number ![]() also satisfies the conditions of the problem, but
also satisfies the conditions of the problem, but ![]() is the least such number.
is the least such number.
4.Solution 1
We note that any number in ![]() can be expressed as
can be expressed as ![]() for some integer
for some integer ![]() . The problem requires that
. The problem requires that ![]() divides this number, and since we know
divides this number, and since we know ![]() divides
divides ![]() , we need that
, we need that ![]() divides 2020. Each number contributes the sum of the digits of
divides 2020. Each number contributes the sum of the digits of ![]() , as well as
, as well as ![]() . Since
. Since ![]() can be prime factorized as
can be prime factorized as ![]() , it has
, it has ![]() factors. So if we sum all the digits of all possible
factors. So if we sum all the digits of all possible ![]() values, and add
values, and add ![]() , we obtain the answer.
, we obtain the answer.
Now we list out all factors of ![]() , or all possible values of
, or all possible values of ![]() .
. ![]() . If we add up these digits, we get
. If we add up these digits, we get ![]() , for a final answer of
, for a final answer of ![]() .
.
-molocyxu
Solution 2 (Official MAA)
Suppose that ![]() has the required property. Then there are positive integers
has the required property. Then there are positive integers ![]() and
and ![]() such that
such that ![]() . Thus
. Thus ![]() , which holds exactly when
, which holds exactly when ![]() is a positive divisor of
is a positive divisor of ![]() The number
The number ![]() has
has ![]() divisors:
divisors: ![]() , and
, and ![]() The requested sum is therefore the sum of the digits in these divisors plus
The requested sum is therefore the sum of the digits in these divisors plus ![]() times the sum of the digits in
times the sum of the digits in ![]() which is
which is![]()
5.Solution 1
Realize that any sequence that works (ascending) can be reversed for descending, so we can just take the amount of sequences that satisfy the ascending condition and multiply by two.
If we choose any of the numbers ![]() through
through ![]() , there are five other spots to put them, so we get
, there are five other spots to put them, so we get ![]() . However, we overcount some cases. Take the example of
. However, we overcount some cases. Take the example of ![]() . We overcount this case because we can remove the
. We overcount this case because we can remove the ![]() or the
or the ![]() . Therefore, any cases with two adjacent numbers swapped is overcounted, so we subtract
. Therefore, any cases with two adjacent numbers swapped is overcounted, so we subtract ![]() cases (namely,
cases (namely, ![]() ,) to get
,) to get ![]() , but we have to add back one more for the original case,
, but we have to add back one more for the original case, ![]() . Therefore, there are
. Therefore, there are ![]() cases. Multiplying by
cases. Multiplying by ![]() gives the desired answer,
gives the desired answer, ![]() .
.
-molocyxu
Solution 2 (Inspired by 2018 CMIMC combo round)
Similar to above, a ![]() correspondence between ascending and descending is established by subtracting each number from
correspondence between ascending and descending is established by subtracting each number from ![]() .
.
We note that the given condition is equivalent to "cycling" ![]() for a contiguous subset of it. For example,
for a contiguous subset of it. For example,
![]()
It's not hard to see that no overcount is possible, and that the cycle is either ![]() "right" or
"right" or ![]() "left." Therefore, we consider how many elements we flip by. If we flip
"left." Therefore, we consider how many elements we flip by. If we flip ![]() or
or ![]() such elements, then there is one way to cycle them. Otherwise, we have
such elements, then there is one way to cycle them. Otherwise, we have ![]() ways. Therefore, the total number of ascending is
ways. Therefore, the total number of ascending is ![]() , and multiplying by two gives
, and multiplying by two gives ![]() ~awang11
~awang11
Solution 3
Similarly to above, we find the number of ascending arrangements and multiply by 2.
We can choose ![]() cards to be the ascending cards, therefore leaving
cards to be the ascending cards, therefore leaving ![]() places to place the remaining card. There are
places to place the remaining card. There are  to do this. However, since the problem is asking for the number of arrangements, we overcount cases such as
to do this. However, since the problem is asking for the number of arrangements, we overcount cases such as ![]() . Notice that the only arrangements that overcount are
. Notice that the only arrangements that overcount are ![]() (case 1) or if two adjacent numbers of
(case 1) or if two adjacent numbers of ![]() are switched (case 2).
are switched (case 2).
![]() This arrangement is counted
This arrangement is counted ![]() times. Each time it is counted for any of the
times. Each time it is counted for any of the ![]() numbers selected. Therefore we need to subtract
numbers selected. Therefore we need to subtract ![]() cases of overcounting.
cases of overcounting.
![]() Each time
Each time ![]() adjacent numbers of switched, there is one overcount. For example, if we have
adjacent numbers of switched, there is one overcount. For example, if we have ![]() , both
, both ![]() or
or ![]() could be removed. Since there are
could be removed. Since there are ![]() possible switches, we need to subtract
possible switches, we need to subtract ![]() cases of overcounting.
cases of overcounting.
Therefore, we have ![]() total arrangements of ascending numbers. We multiply by two (for descending) to get the answer of
total arrangements of ascending numbers. We multiply by two (for descending) to get the answer of ![]() -PCChess
-PCChess
Solution 4 (No overcounting)
Like in previous solutions, we will count the number of ascending arrangements and multiply by 2.
First, consider the arrangement 1-2-3-4-5-6. That gives us 1 arrangement which works.
Next, we can switch two adjacent cards. There are 5 ways to pick two adjacent cards, so this gives us 5 arrangements.
Now, we can "cycle" 3 adjacent cards. For example, 1-2-3 becomes 2-3-1 which becomes 3-1-2. There are 4 ways to pick a set of 3 adjacent cards, so this gives us 4x2=8 arrangements.
Cycling 4 adjacent cards, we get the new arrangements 2-3-4-1 (which works,) 3-4-1-2 (which doesn't work,) and 4-1-2-3 (which does work.) We get 6 arrangements.
Similarly, when cycling 5 cards, we find 2x2=4 arrangements, and when cycling 6 cards, we find 2x1=2 arrangements.
Adding, we figure out that there are 1+5+8+6+4+2=26 ascending arrangements. Multiplying by 2, we get the answer ![]() -i8Pie
-i8Pie
Solution 5 (Official MAA 1)
First count the number of permutations of the cards such that if one card is removed, the remaining cards will be in ascending order. There is ![]() such permutation where all the cards appear in order:
such permutation where all the cards appear in order: ![]() There are
There are ![]() such permutations where two adjacent cards are interchanged, as in
such permutations where two adjacent cards are interchanged, as in ![]() The other such permutations arise from removing one card from
The other such permutations arise from removing one card from ![]() and placing it in a position at least two away from its starting location. There are
and placing it in a position at least two away from its starting location. There are ![]() such positions to place each of the cards numbered
such positions to place each of the cards numbered ![]() and
and ![]() and
and ![]() such positions for each of the cards numbered
such positions for each of the cards numbered ![]() and
and ![]() This accounts for
This accounts for ![]() permutations. Thus there are
permutations. Thus there are ![]() permutations where one card can be removed so that the remaining cards are in ascending order. There is an equal number of permutations that result in the cards' being in descending order. This gives the total
permutations where one card can be removed so that the remaining cards are in ascending order. There is an equal number of permutations that result in the cards' being in descending order. This gives the total ![]() .
.
Solution 6 (Official MAA 2)
More generally, suppose there are ![]() cards numbered
cards numbered ![]() arranged in ascending order. If any one of the
arranged in ascending order. If any one of the ![]() cards is removed and placed in one of the
cards is removed and placed in one of the ![]() positions in the arrangement, the resulting permutation will have the property that one card can be removed so that the remaining cards are in ascending order. This accounts for
positions in the arrangement, the resulting permutation will have the property that one card can be removed so that the remaining cards are in ascending order. This accounts for ![]() permutations. However, the original ascending order has been counted
permutations. However, the original ascending order has been counted ![]() times, and each order that arises by switching two neighboring cards has been counted twice. Hence the number of arrangements where one card can be removed resulting in the remaining cards' being in ascending order is
times, and each order that arises by switching two neighboring cards has been counted twice. Hence the number of arrangements where one card can be removed resulting in the remaining cards' being in ascending order is ![]() When
When ![]() , this is
, this is ![]() , and the final answer is
, and the final answer is ![]() .
.
Solution 7 (Simple and Easy, don't know why it's hard)
For ascending you can place the ![]() in
in ![]() locations and the rest of the numbers in
locations and the rest of the numbers in ![]() locations based on the sequence
locations based on the sequence ![]() .
. ![]() . Multiply by
. Multiply by ![]() to account for the descending and get
to account for the descending and get ![]() . ~Lopkiloinm
. ~Lopkiloinm
6.Solution 1
![[asy] size(10cm); pair A, B, C, D, O, P, H, L, X, Y; A = (-1, 0); B = (1, 0); H = (0, 0); C = (5, 0); D = (9, 0); L = (7, 0); O = (0, sqrt(160/13 - 1)); P = (7, sqrt(160/13 - 4)); X = (0, sqrt(160/13 - 4)); Y = (O + P) / 2; draw(A -- O -- B -- cycle); draw(C -- P -- D -- cycle); draw(B -- C); draw(O -- P); draw(P -- X, dashed); draw(O -- H, dashed); draw(P -- L, dashed); draw(circle(O, sqrt(160/13))); draw(circle(P, sqrt(160/13))); path b = brace(L, H); draw(b); label("$R$", O -- Y, N); label("$R$", Y -- P, N); label("$R$", O -- A, NW); label("$R$", P -- D, NE); label("$1$", A -- H, N); label("$2$", L -- D, N); label("$7$", b, S); [/asy]](https://latex.artofproblemsolving.com/a/1/5/a156f24285b03d26c18745c310c33b11767325d5.png)
Set the common radius to ![]() . First, take the cross section of the sphere sitting in the hole of radius 1. If we draw the perpendicular bisector of the chord (the hole) through the circle, this line goes through the center. Connect the center also to where the chord hits the circle, for a right triangle with hypotenuse
. First, take the cross section of the sphere sitting in the hole of radius 1. If we draw the perpendicular bisector of the chord (the hole) through the circle, this line goes through the center. Connect the center also to where the chord hits the circle, for a right triangle with hypotenuse ![]() and base
and base ![]() . Therefore, the height of this circle outside of the hole is
. Therefore, the height of this circle outside of the hole is ![]() .
.
The other circle follows similarly for a height (outside the hole) of ![]() . Now, if we take the cross section of the entire board, essentially making it 2-D, we can connect the centers of the two spheres, then form another right triangle with base
. Now, if we take the cross section of the entire board, essentially making it 2-D, we can connect the centers of the two spheres, then form another right triangle with base ![]() , as given by the problem. The height of this triangle is the difference between the heights of the parts of the two spheres outside the holes, which is
, as given by the problem. The height of this triangle is the difference between the heights of the parts of the two spheres outside the holes, which is ![]() . Now we can set up an equation in terms of
. Now we can set up an equation in terms of ![]() with the Pythagorean theorem:
with the Pythagorean theorem:![]() Simplifying a few times,
Simplifying a few times,![]()
![]()
![]()
![]()
![]()
![]() Therefore, our answer is
Therefore, our answer is ![]() .
.
-molocyxu
Solution 2 (Official MAA)
Consider a cross section of the board and spheres with a plane that passes through the centers of the holes and centers of the spheres as shown.
![[asy] unitsize(1.5 cm); pair A, B, C, D, E, F, G, P, Q; C = dir(175); D = dir(175 + 180); P = (-2,-0.8); Q = (2,-0.8); A = (C + reflect(P,Q)*(C))/2; B = (D + reflect(P,Q)*(D))/2; E = intersectionpoint(P--A, Circle(C,1)); F = intersectionpoint(B--Q, Circle(D,1)); G = (D + reflect(A,C)*(D))/2; draw(Circle(C,1)); draw(Circle(D,1)); draw(P--Q); draw(A--(C + (0,1))); draw(B--(D + (0,1))); draw(E--C--D--F); draw(D--G); dot("$A$", A, NE); dot("$B$", B, NW); dot("$C$", C, NW); dot("$D$", D, NE); dot("$E$", E, SW); dot("$F$", F, SE); dot("$G$", G, SE); [/asy]](https://latex.artofproblemsolving.com/f/e/4/fe4574167ae6aa4915cecb717aac9e0b04246ea5.png)
Let ![]() ,
, ![]() , and
, and ![]() be, respectively, the center of the hole with radius
be, respectively, the center of the hole with radius ![]() the center of the sphere resting in that hole, and a point on the edge of that hole. Let
the center of the sphere resting in that hole, and a point on the edge of that hole. Let ![]() ,
, ![]() , and
, and ![]() be the corresponding points for the hole with radius
be the corresponding points for the hole with radius ![]() Let
Let ![]() be the point on
be the point on ![]() such that
such that ![]() . Let the radius of the spheres be
. Let the radius of the spheres be ![]() . Because
. Because ![]() and
and ![]() , it follows that
, it follows that![]() Because
Because ![]() ,
, ![]() , and
, and ![]() , it follows that
, it follows that![]() which simplifies to
which simplifies to ![]() . The requested sum is
. The requested sum is ![]() . The value of
. The value of ![]() is approximately
is approximately ![]()
7.Solution 1
Let ![]() be the number of women selected. Then, the number of men not selected is
be the number of women selected. Then, the number of men not selected is ![]() . Note that the sum of the number of women selected and the number of men not selected is constant at
. Note that the sum of the number of women selected and the number of men not selected is constant at ![]() . Each combination of women selected and men not selected corresponds to a committee selection. Since choosing 12 individuals from the total of 23 would give
. Each combination of women selected and men not selected corresponds to a committee selection. Since choosing 12 individuals from the total of 23 would give ![]() women and
women and ![]() men, the number of committee selections is
men, the number of committee selections is ![]() . The answer is
. The answer is ![]() . ~awang11's sol
. ~awang11's sol
Solution 2 (Bash)
We casework on the amount of men on the committee.
If there are no men in the committee, there are ![]() ways to pick the women on the committee, for a total of
ways to pick the women on the committee, for a total of  . Notice that
. Notice that ![]() is equal to
is equal to ![]() , so the case where no men are picked can be grouped with the case where all men are picked. When all men are picked, all females must also be picked, for a total of
, so the case where no men are picked can be grouped with the case where all men are picked. When all men are picked, all females must also be picked, for a total of ![]() . Therefore, these cases can be combined to
. Therefore, these cases can be combined to![\[\dbinom{11}{0} \cdot \left(\dbinom{12}{1} + \dbinom{12}{12}\right)\]](https://latex.artofproblemsolving.com/9/9/d/99db714072c938e8a97e356004110de9e2fb047d.png) Since
Since  , and
, and  , we can further simplify this to
, we can further simplify this to![\[\dbinom{11}{0} \cdot \dbinom{13}{1}\]](https://latex.artofproblemsolving.com/1/2/a/12a522ac0cf7513e837f3e2459d5d3aac4e161b9.png)
All other cases proceed similarly. For example, the case with one men or ten men is equal to  . Now, if we factor out a
. Now, if we factor out a ![]() , then all cases except the first two have a factor of
, then all cases except the first two have a factor of ![]() , so we can factor this out too to make our computation slightly easier. The first two cases (with
, so we can factor this out too to make our computation slightly easier. The first two cases (with ![]() factored out) give
factored out) give ![]() , and the rest gives
, and the rest gives ![]() . Adding the
. Adding the ![]() gives
gives ![]() . Now, we can test for prime factors. We know there is a factor of
. Now, we can test for prime factors. We know there is a factor of ![]() , and the rest is
, and the rest is ![]() . We can also factor out a
. We can also factor out a ![]() , for
, for ![]() , and the rest is
, and the rest is ![]() . Adding up all the prime factors gives
. Adding up all the prime factors gives ![]() .
.
Solution 3 (Vandermonde's identity)
Applying Vandermonde's identity by setting ![]() ,
, ![]() , and
, and ![]() , we obtain
, we obtain 
![]() . ~Lcz
. ~Lcz
Short Proof
Consider the following setup:![[asy] size(1000, 100); for(int i=0; i<23; ++i){ dot((i, 0)); } draw((10.5, -1.5)--(10.5, 1.5), dashed); [/asy]](https://latex.artofproblemsolving.com/1/a/7/1a7ec8160e9e17afe12660418c09e229455b0274.png) The dots to the left represent the men, and the dots to the right represent the women. Now, suppose we put a mark on
The dots to the left represent the men, and the dots to the right represent the women. Now, suppose we put a mark on ![]() people (the
people (the ![]() ). Those to the left of the dashed line get to be "in" on the committee if they have a mark. Those on the right side of the dashed line are already on the committee, but if they're marked they get forcibly evicted from it. If there were
). Those to the left of the dashed line get to be "in" on the committee if they have a mark. Those on the right side of the dashed line are already on the committee, but if they're marked they get forcibly evicted from it. If there were ![]() people marked on the left, there ends up being
people marked on the left, there ends up being ![]() people not marked on the right. Circles represent those in the committee.
people not marked on the right. Circles represent those in the committee.![[asy] size(1000, 100); for(int i=0; i<23; ++i){ dot((i, 0)); } for(int i=0; i<23; ++i){ if(i%2==0){ if(i >= 11){ draw(circle((i, 0), 0.25)); } continue; } label("$*$", (i,0.5), N); if(i < 11){ draw(circle((i, 0), 0.25)); } } draw((10.5, -1.5)--(10.5, 1.5), dashed); [/asy]](https://latex.artofproblemsolving.com/0/b/2/0b2c25bdce435033db79017c4b6b049a6f2e25f3.png)
We have our bijection, so the number of ways will be ![]() .
.
~programjames1
Solution 4
Notice that the committee can consist of ![]() boys and
boys and ![]() girls. Summing over all possible
girls. Summing over all possible ![]() gives
gives![\[\sum_{k=0}^{11}\binom{11}{k}\binom{12}{k+1}=\binom{11}{0}\binom{12}{1}+\binom{11}{1}\binom{12}{2}+\cdots + \binom{11}{11}\binom{12}{12}\]](https://latex.artofproblemsolving.com/e/3/1/e310df84529303ec7abfe238f7c6241b7da2552d.png) Using the identity
Using the identity  , and Pascal's Identity
, and Pascal's Identity  , we get
, we get![\[\sum_{k=0}^{11}\binom{11}{k}\binom{12}{k+1}=\binom{12}{12}+\binom{12}{1}\left(\binom{11}{0}+\binom{11}{1}\right)+\cdots\]](https://latex.artofproblemsolving.com/0/5/f/05f8c82792e7835eadbbc64ef5bc1b333b1398e1.png)
![\[=\binom{12}{0}^2+\binom{12}{1}^2+\binom{12}{2}^2+\binom{12}{3}^2+\binom{12}{4}^2+\binom{12}{5}^2+\frac{\binom{12}{6}^2}{2}\]](https://latex.artofproblemsolving.com/1/0/1/1018226ff46f0a60bb07e43a1d38a6cda03f23f3.png)
![\[=\frac{1}{2}\sum_{k=0}^{12}\binom{12}{k}^2\]](https://latex.artofproblemsolving.com/1/d/7/1d7ff8ef7a27271f6bb378fc985f500ec072c946.png) Using the identity
Using the identity  , this simplifies to
, this simplifies to![\[\frac{1}{2}\cdot \binom{24}{12}=\frac{24\cdot 23\cdot 22\cdot 21\cdot 20\cdot 19\cdot 18\cdot 17\cdot 16\cdot 15\cdot 14\cdot 13}{2\cdot 12\cdot 11\cdot 10\cdot 9\cdot 8\cdot 7\cdot 6\cdot 5\cdot 4\cdot 3\cdot 2}=2\cdot 7\cdot 13\cdot 17\cdot 19\cdot 23\]](https://latex.artofproblemsolving.com/6/7/b/67be4ef888adc44adfd48764c259a9f7948faeaa.png) so the desired answer is
so the desired answer is ![]() ~ktong
~ktong
Solution 5 (Official MAA)
Select any ![]() club members. That group will have
club members. That group will have ![]() men and
men and ![]() women, so the number of women in the club not selected in that group is
women, so the number of women in the club not selected in that group is ![]() . Thus, if the committee includes the men who were selected and the women who were not selected, the committee would have the correct number of men and women. Conversely, for every committee that could be formed with
. Thus, if the committee includes the men who were selected and the women who were not selected, the committee would have the correct number of men and women. Conversely, for every committee that could be formed with ![]() men and
men and ![]() women, the men on this committee together with the women not on the committee comprise a subset of
women, the men on this committee together with the women not on the committee comprise a subset of ![]() club members. Thus
club members. Thus![\[N = \binom{23}{11}= \frac{23\cdot22\cdot21\cdot20\cdot19\cdot18\cdot17\cdot16\cdot15\cdot14\cdot13}{11\cdot10\cdot9\cdot8\cdot7\cdot6\cdot5\cdot4\cdot3\cdot2\cdot1}=23\cdot19\cdot17\cdot13\cdot7\cdot2.\]](https://latex.artofproblemsolving.com/e/8/9/e892ea5f38e9f018f0ebf2c198d16518d6279505.png) The requested sum is
The requested sum is ![]()
8.Solution 1 (Coordinates)
![[asy] size(8cm); pair O, A, B, C, D, F, G, P, X; O = (0, 0); A = (5, 0); X = (8, 0); P = (5, 5 / sqrt(3)); B = rotate(-120, A) * ((O + A) / 2); C = rotate(-120, B) * ((A + B) / 2); D = rotate(-120, C) * ((B + C) / 2); F = rotate(-120, D) * ((C + D) / 2); G = rotate(-120, F) * ((D + F) / 2); draw(O -- A -- B -- C -- D -- F -- G); draw(A -- X, dashed); markscalefactor = 0.05; path angle = anglemark(X, A, B); draw(angle); dot(P); dot(O); label("$O$", O, W); label("$P$", P, E); label("$60^\circ$", angle, ENE*3); [/asy]](https://latex.artofproblemsolving.com/2/a/1/2a1b70a72018476e9501ee736e2b3fd58ee841a0.png)
We plot this on the coordinate grid with point ![]() as the origin. We will keep a tally of the x-coordinate and y-coordinate separately.
as the origin. We will keep a tally of the x-coordinate and y-coordinate separately.
First move: The ant moves right ![]() . Second move: We use properties of a
. Second move: We use properties of a ![]() triangle to get
triangle to get ![]() right,
right, ![]() up. Third move:
up. Third move: ![]() left,
left, ![]() up. Fourth move:
up. Fourth move: ![]() left. Fifth move:
left. Fifth move: ![]() left,
left, ![]() down. Sixth move:
down. Sixth move: ![]() right,
right, ![]() down.
down.
Total of x-coordinate: ![]() . Total of y-coordinate:
. Total of y-coordinate: ![]() .
.
After this cycle of six moves, all moves repeat with a factor of ![]() . Using the formula for a geometric series, multiplying each sequence by
. Using the formula for a geometric series, multiplying each sequence by ![]() will give us the point
will give us the point ![]() .
.
![]() ,
, ![]() . Therefore, the coordinates of point
. Therefore, the coordinates of point ![]() are
are ![]() , so using the Pythagorean Theorem,
, so using the Pythagorean Theorem, ![]() , for an answer of
, for an answer of ![]() .
.
-molocyxu
Solution 2 (Complex)
We place the ant at the origin of the complex plane with its first move being in the positive real direction. Then the ant's journey can be represented as the infinite series![\[5\left(1 + \frac{e^{\frac{i\pi}{3}}}{2} + \left(\frac{e^{\frac{i\pi}{3}}}{2}\right)^2 + \cdots\right)\]](https://latex.artofproblemsolving.com/a/7/b/a7bc5ebcae36c2fdcee111556cce2a2198ea0b45.png) Using the formula for an infinite geometric series, this is equal to
Using the formula for an infinite geometric series, this is equal to![\[\frac{5}{1 - \frac12e^{\frac{i\pi}{3}}} = \frac{5}{1 - \frac{1 + i\sqrt{3}}{4}} = \frac{20}{3 - i\sqrt{3}} = 5 + \frac{5i\sqrt{3}}{3}\]](https://latex.artofproblemsolving.com/d/a/1/da14fb0a1f31c2a9f515de2c38f990df612132ce.png) We are looking for the square of the modulus of this value:
We are looking for the square of the modulus of this value:![\[\left|\frac{5 + 5i\sqrt{3}}{3}\right|^2 = 25 + \frac{25}{3} = \frac{100}{3}\]](https://latex.artofproblemsolving.com/4/8/d/48da52b0c439e0d27489a79949ad8678ae6b6008.png) so the answer is
so the answer is ![]() .
.
Solution 3 (Solution 1 faster)
The ant goes in the opposite direction every ![]() moves, going
moves, going ![]() the distance backwards. Using geometric series, he travels
the distance backwards. Using geometric series, he travels ![]() the distance of the first three moves over infinity moves. Now, we use coordinates meaning
the distance of the first three moves over infinity moves. Now, we use coordinates meaning ![]() or
or ![]() . Multiplying these by
. Multiplying these by ![]() , we get
, we get ![]()
![]()
![]() .
.
~Lcz
Solution 4 (Official MAA 1)
Suppose that the bug starts at the origin ![]() and travels a distance of
and travels a distance of ![]() units due east on the first day, and that there is a real number
units due east on the first day, and that there is a real number ![]() with
with ![]() such that each day after the first, the bug walks
such that each day after the first, the bug walks ![]() times as far as the previous day. On day
times as far as the previous day. On day ![]() , the bug travels along the vector
, the bug travels along the vector ![]() that has magnitude
that has magnitude ![]() and direction
and direction ![]() . Then
. Then ![]() is the terminal point of the infinite sum of the vectors
is the terminal point of the infinite sum of the vectors ![]() . The
. The ![]() -coordinate of this sum is
-coordinate of this sum is![]()
![]() Because the angles repeat after 6 terms, this sum is equal to
Because the angles repeat after 6 terms, this sum is equal to![]() where
where![]() Similarly, the
Similarly, the ![]() -coordinate of
-coordinate of ![]() will be
will be ![]() , where
, where![]() In this case
In this case ![]() and
and ![]() , so
, so![]()
![]() and the coordinates of
and the coordinates of ![]() are
are![\[\left(\frac{5S}{1-\frac1{64}}, \frac{5T}{1-\frac1{64}}\right)=\left(5,\frac{5\sqrt3}{3}\right).\]](https://latex.artofproblemsolving.com/8/4/4/8448ad766c5ef223e19361d2fe7cbe6686703ae8.png) Thus the square of the distance from the origin to
Thus the square of the distance from the origin to ![]() is
is ![]() . The requested sum is
. The requested sum is ![]() .
.
Solution 5 (Official MAA 2)
Let point ![]() be the origin in the complex plane. Point
be the origin in the complex plane. Point ![]() is the complex sum
is the complex sum ![]() , where
, where ![]() . The distance squared is
. The distance squared is![\[{OP}^2=\left|\frac5{1-\frac{1+i\sqrt3}4}\right|^{2}= \frac{(4\cdot5)^2}{\left|4-(1+i\sqrt3)\right|^2}=\frac{400}{9+3}=\frac{100}3.\]](https://latex.artofproblemsolving.com/4/6/2/462579a70da1183d98df3ea371a32622c05d6817.png)
9.Solution 1
![[asy] size(12cm); for (int x = 1; x < 18; ++x) { draw((x, 0) -- (x, 9), dotted); } for (int y = 1; y < 9; ++y) { draw((0, y) -- (18, y), dotted); } draw((0, 0) -- (18, 0) -- (18, 9) -- (0, 9) -- cycle); pair b1, b2, b3; pair c1, c2, c3; pair a1, a2, a3; b1 = (3, 0); b2 = (12, 0); b3 = (16, 0); c1 = (0, 2); c2 = (0, 4); c3 = (0, 8); a1 = b1 + c1; a2 = b2 + c2; a3 = b3 + c3; draw(b1 -- a1 -- c1); draw(b2 -- a2 -- c2); draw(b3 -- a3 -- c3); dot(a1); dot(a2); dot(a3); label("$a_1$", a1, NE); label("$a_2$", a2, NE); label("$a_3$", a3, NE); label("$b_1$", b1, S); label("$b_2$", b2, S); label("$b_3$", b3, S); label("$c_1$", c1, W); label("$c_2$", c2, W); label("$c_3$", c3, W); [/asy]](https://latex.artofproblemsolving.com/b/8/9/b897aa5312f48ded1d6fa21afb4acfef70453ad3.png)
First, prime factorize ![]() as
as ![]() . Denote
. Denote ![]() as
as ![]() ,
, ![]() as
as ![]() , and
, and ![]() as
as ![]() .
.
In order for ![]() to divide
to divide ![]() , and for
, and for ![]() to divide
to divide ![]() ,
, ![]() , and
, and ![]() . We will consider each case separately. Note that the total amount of possibilities is
. We will consider each case separately. Note that the total amount of possibilities is ![]() , as there are
, as there are ![]() choices for each factor.
choices for each factor.
We notice that if we add ![]() to
to ![]() and
and ![]() to
to ![]() , then we can reach the stronger inequality
, then we can reach the stronger inequality ![]() . Therefore, if we pick
. Therefore, if we pick ![]() integers from
integers from ![]() to
to ![]() , they will correspond to a unique solution, forming a 1-1 correspondence between the numbers
, they will correspond to a unique solution, forming a 1-1 correspondence between the numbers ![]() ,
, ![]() , and
, and ![]() . This is also equivalent to applying stars and bars on distributing the powers of 2 and 5 through differences. The amount of solutions to this inequality is
. This is also equivalent to applying stars and bars on distributing the powers of 2 and 5 through differences. The amount of solutions to this inequality is ![]() .
.
The case for ![]() ,
,![]() , and
, and ![]() proceeds similarly for a result of
proceeds similarly for a result of ![]() . Therefore, the probability of choosing three such factors is
. Therefore, the probability of choosing three such factors is![\[\frac{\dbinom{21}{3} \cdot \dbinom{12}{3}}{190^3}.\]](https://latex.artofproblemsolving.com/8/1/7/817cd42178e0b531ab9f976e36422ecf8aff72e1.png) Simplification gives
Simplification gives ![]() , and therefore the answer is
, and therefore the answer is ![]() .
.
-molocyxu
Solution 2
Same as before, say the factors have powers of ![]() and
and ![]() .
. ![]() can either be all distinct, all equal, or two of the three are equal. As well, we must have
can either be all distinct, all equal, or two of the three are equal. As well, we must have ![]() . If they are all distinct, the number of cases is simply
. If they are all distinct, the number of cases is simply ![]() . If they are all equal, there are only
. If they are all equal, there are only ![]() cases for the general value. If we have a pair equal, then we have
cases for the general value. If we have a pair equal, then we have  . We need to multiply by
. We need to multiply by ![]() because if we have two values
because if we have two values ![]() , we can have either
, we can have either ![]() or
or ![]() .
.
![\[{19 \choose 3} + 2 \cdot {19 \choose 2} + 19 = 1330\]](https://latex.artofproblemsolving.com/b/6/9/b6964a39cac249e2ec85607429575ab892582bac.png)
Likewise for ![]() , we get
, we get
![\[{10 \choose 3} + 2 \cdot {10 \choose 2} + 10 = 220\]](https://latex.artofproblemsolving.com/e/4/2/e42e04f664322ecd8bdbda8a537c417de766c199.png)
The final probability is simply ![]() . Simplification gives
. Simplification gives ![]() , and therefore the answer is
, and therefore the answer is ![]() .
.
Solution 3
Similar to before, we calculate that there are ![]() ways to choose
ways to choose ![]() factors with replacement. Then, we figure out the number of triplets
factors with replacement. Then, we figure out the number of triplets ![]() and
and ![]() , where
, where ![]() ,
, ![]() , and
, and ![]() represent powers of
represent powers of ![]() and
and ![]() ,
, ![]() , and
, and ![]() represent powers of
represent powers of ![]() , such that the triplets are in non-descending order. The maximum power of
, such that the triplets are in non-descending order. The maximum power of ![]() is
is ![]() , and the maximum power of
, and the maximum power of ![]() is
is ![]() . Using the Hockey Stick identity, we figure out that there are
. Using the Hockey Stick identity, we figure out that there are ![]() ways to choose
ways to choose ![]() ,
, ![]() and
and ![]() , and
, and ![]() ways to choose
ways to choose ![]() ,
, ![]() , and
, and ![]() . Therefore, the probability of choosing
. Therefore, the probability of choosing ![]() factors which satisfy the conditions is
factors which satisfy the conditions is![\[\frac{\dbinom{21}{3} \cdot \dbinom{12}{3}}{190^3}.\]](https://latex.artofproblemsolving.com/8/1/7/817cd42178e0b531ab9f976e36422ecf8aff72e1.png) This simplifies to
This simplifies to ![]() , therefore
, therefore ![]()
![]() .
.
10.Solution 1
Taking inspiration from ![]() we are inspired to take
we are inspired to take ![]() to be
to be ![]() , the lowest prime not dividing
, the lowest prime not dividing ![]() , or
, or ![]() . Now, there are
. Now, there are ![]() factors of
factors of ![]() , so
, so ![]() , and then
, and then ![]() for
for ![]() . Now,
. Now, ![]() . Noting
. Noting ![]() is the minimal that satisfies this, we get
is the minimal that satisfies this, we get ![]() . Thus, it is easy to verify this is minimal and we get
. Thus, it is easy to verify this is minimal and we get ![]() . ~awang11
. ~awang11
Solution 2
Assume for the sake of contradiction that ![]() is a multiple of a single digit prime number, then
is a multiple of a single digit prime number, then ![]() must also be a multiple of that single digit prime number to accommodate for
must also be a multiple of that single digit prime number to accommodate for ![]() . However that means that
. However that means that ![]() is divisible by that single digit prime number, which violates
is divisible by that single digit prime number, which violates ![]() , so contradiction.
, so contradiction.
![]() is also not 1 because then
is also not 1 because then ![]() would be a multiple of it.
would be a multiple of it.
Thus, ![]() is a multiple of 11 and/or 13 and/or 17 and/or...
is a multiple of 11 and/or 13 and/or 17 and/or...
Assume for the sake of contradiction that ![]() has at most 1 power of 11, at most 1 power of 13...and so on... Then, for
has at most 1 power of 11, at most 1 power of 13...and so on... Then, for ![]() to be satisfied,
to be satisfied, ![]() must contain at least the same prime factors that
must contain at least the same prime factors that ![]() has. This tells us that for the primes where
has. This tells us that for the primes where ![]() has one power of,
has one power of, ![]() also has at least one power, and since this holds true for all the primes of
also has at least one power, and since this holds true for all the primes of ![]() ,
, ![]() . Contradiction.
. Contradiction.
Thus ![]() needs more than one power of some prime. The obvious smallest possible value of
needs more than one power of some prime. The obvious smallest possible value of ![]() now is
now is ![]() . Since
. Since ![]() , we need
, we need ![]() to be a multiple of 11 at least
to be a multiple of 11 at least ![]() that is not divisible by
that is not divisible by ![]() and most importantly,
and most importantly, ![]() .
. ![]() is divisible by
is divisible by ![]() , out.
, out. ![]() is divisible by 2, out.
is divisible by 2, out. ![]() is divisible by 5, out.
is divisible by 5, out. ![]() is divisible by 2, out.
is divisible by 2, out. ![]() and satisfies all the conditions in the given problem, and the next case
and satisfies all the conditions in the given problem, and the next case ![]() will give us at least
will give us at least ![]() , so we get
, so we get ![]() .
.
11.Solution 1 (Strategic Casework)
Either ![]() or not. If it is, note that Vieta's forces
or not. If it is, note that Vieta's forces ![]() . Then,
. Then, ![]() can be anything. However,
can be anything. However, ![]() can also be anything, as we can set the root of
can also be anything, as we can set the root of ![]() (not equal to
(not equal to ![]() ) to any integer, producing a possible integer value of
) to any integer, producing a possible integer value of ![]() . Therefore there are
. Therefore there are ![]() in this case*. If it isn't, then
in this case*. If it isn't, then ![]() are the roots of
are the roots of ![]() . This means by Vieta's, that:
. This means by Vieta's, that:
![]()
![]()
![]()
Solving these inequalities while considering that ![]() to prevent
to prevent ![]() , we obtain
, we obtain ![]() possible tuples and adding gives
possible tuples and adding gives ![]() . ~awang11
. ~awang11
Solution 2 (Bash)
Define ![]() . Since
. Since ![]() , we know
, we know ![]() . Plugging in
. Plugging in ![]() into
into ![]() , we get
, we get ![]() . Setting
. Setting ![]() ,
,![]() . Simplifying and cancelling terms,
. Simplifying and cancelling terms,![]()
![]()
![]()
![]()
![]()
![]()
Therefore, either ![]() or
or ![]() . The first case is easy:
. The first case is easy: ![]() and there are
and there are ![]() tuples in that case. In the second case, we simply perform casework on even values of
tuples in that case. In the second case, we simply perform casework on even values of ![]() , to get
, to get ![]() tuples, subtracting the
tuples, subtracting the ![]() tuples in both cases we get
tuples in both cases we get ![]() .
.
-EZmath2006
Notes For *
In case anyone is confused by this (as I initially was). In the case where ![]() , this does not mean that g has a double root of
, this does not mean that g has a double root of ![]() , ONLY that
, ONLY that ![]() is one of the roots of g. So basically since
is one of the roots of g. So basically since ![]() in this case,
in this case, ![]() , and we have
, and we have ![]() choices for b and we still can ensure c is an integer with absolute value less than or equal to 10 simply by having another integer root of g that when added to
choices for b and we still can ensure c is an integer with absolute value less than or equal to 10 simply by having another integer root of g that when added to ![]() ensures this, and of course an integer multiplied by an integer is an integer so
ensures this, and of course an integer multiplied by an integer is an integer so ![]() will still be an integer. In other words, you have can have
will still be an integer. In other words, you have can have ![]() and
and ![]() be any integer with absolute value less than or equal to 10 with
be any integer with absolute value less than or equal to 10 with ![]() still being an integer. Now refer back to the 1st solution. ~First
still being an integer. Now refer back to the 1st solution. ~First
12.Solution 1
Lifting the Exponent shows that![]() so thus,
so thus, ![]() divides
divides ![]() . It also shows that
. It also shows that![]() so thus,
so thus, ![]() divides
divides ![]() .
.
Now, multiplying ![]() by
by ![]() , we see
, we see![]() and since
and since ![]() and
and ![]() then
then ![]() meaning that we have that by LTE,
meaning that we have that by LTE, ![]() divides
divides ![]() .
.
Since ![]() ,
, ![]() and
and ![]() all divide
all divide ![]() , the smallest value of
, the smallest value of ![]() working is their LCM, also
working is their LCM, also ![]() . Thus the number of divisors is
. Thus the number of divisors is ![]() .
.
~kevinmathz
Solution 2 (Simpler, just basic mods and Fermat's theorem)
Note that for all ![]() ,
, ![]() is divisible by
is divisible by ![]() because that is a factor. That is
because that is a factor. That is ![]() , so now we can clearly see that the smallest
, so now we can clearly see that the smallest ![]() to make the expression divisible by
to make the expression divisible by ![]() is just
is just ![]() . Similarly, we can reason that the smallest
. Similarly, we can reason that the smallest ![]() to make the expression divisible by
to make the expression divisible by ![]() is just
is just ![]() .
.
Finally, for ![]() , take
, take ![]() and
and ![]() of each quantity (They happen to both be
of each quantity (They happen to both be ![]() and
and ![]() respectively, so you only need to compute once). One knows from Fermat's theorem that the maximum possible minimum
respectively, so you only need to compute once). One knows from Fermat's theorem that the maximum possible minimum ![]() for divisibility by
for divisibility by ![]() is
is ![]() , and other values are factors of
, and other values are factors of ![]() . Testing all of them(just
. Testing all of them(just ![]() ,
,![]() ,
,![]() using mods-not too bad),
using mods-not too bad), ![]() is indeed the smallest value to make the expression divisible by
is indeed the smallest value to make the expression divisible by ![]() , and this clearly is NOT divisible by
, and this clearly is NOT divisible by ![]() . Therefore, the smallest
. Therefore, the smallest ![]() to make this expression divisible by
to make this expression divisible by ![]() is
is ![]() .
.
Calculating the LCM of all these, one gets ![]() . Using the factor counting formula, the answer is
. Using the factor counting formula, the answer is ![]() =
= ![]() .
.
~Solution by thanosaops
~formatted by MY-2
~also formatted by pandyhu2001
Solution 3 (Elementary and Thorough)
As usual, denote ![]() the highest power of prime
the highest power of prime ![]() that divides
that divides ![]() . For divisibility by
. For divisibility by ![]() , notice that
, notice that ![]() as
as ![]()
![]() , and upon checking mods,
, and upon checking mods, ![]() is divisible by
is divisible by ![]() but not
but not ![]() . In addition,
. In addition, ![]() is divisible by
is divisible by ![]() because
because ![]() , and the rightmost factor equates to
, and the rightmost factor equates to ![]() . In fact,
. In fact, ![]() is the least possible choice to ensure divisibility by
is the least possible choice to ensure divisibility by ![]() because if
because if ![]() , with
, with ![]() and
and ![]() , we write
, we write![]() Then, the rightmost factor is equivalent to
Then, the rightmost factor is equivalent to ![]() , and
, and ![]() .
.
For divisibility by ![]() , we'll induct, claiming that
, we'll induct, claiming that ![]() for whole numbers
for whole numbers ![]() . The base case is clear. Then,
. The base case is clear. Then,![]() By the induction hypothesis,
By the induction hypothesis, ![]() . Then, notice that
. Then, notice that![]() This tells us that
This tells us that ![]() is divisible by
is divisible by ![]() , but not
, but not ![]() so that
so that ![]() , completing our induction. We can verify that
, completing our induction. We can verify that ![]() is the least choice of
is the least choice of ![]() to ensure divisibility by
to ensure divisibility by ![]() by arguing similarly to the
by arguing similarly to the ![]() case.
case.
Finally, for ![]() , we take the powers of
, we take the powers of ![]() and
and ![]() in mod
in mod ![]() and mod
and mod ![]() . Writing out these mods, we have that
. Writing out these mods, we have that ![]() if and only if
if and only if ![]() , in which
, in which ![]() . So here we claim that
. So here we claim that ![]() and perform yet another induction. The base case is true:
and perform yet another induction. The base case is true: ![]() , but
, but ![]() . Now then, assuming the induction statement to hold for some
. Now then, assuming the induction statement to hold for some ![]() ,
,![]() Note that
Note that ![]() equates to
equates to ![]() in both mod
in both mod ![]() and mod
and mod ![]() . We notice that
. We notice that ![]() . Writing out the powers of
. Writing out the powers of ![]() mod
mod ![]() , we have
, we have ![]() . Also
. Also ![]() when
when ![]() is a multiple of
is a multiple of ![]() . Hence for
. Hence for ![]() ,
, ![]() . Thus,
. Thus, ![]() , completing our induction. Applying the same argument from the previous two cases,
, completing our induction. Applying the same argument from the previous two cases, ![]() is the least choice to ensure divisibility by
is the least choice to ensure divisibility by ![]() .
.
Our answer is the number of divisors of ![]() . It is
. It is ![]() .
.
~hnkevin42
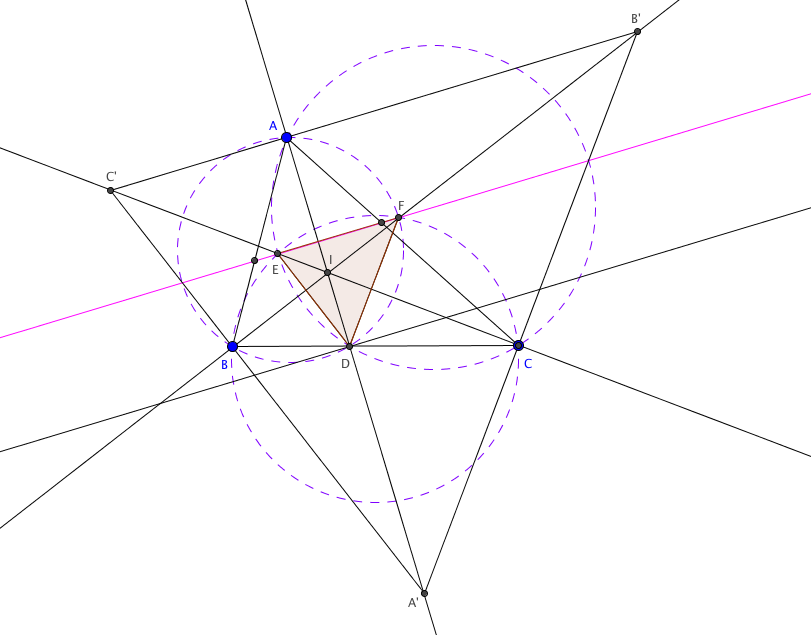
13.Solution 1
Points are defined as shown. It is pretty easy to show that ![]() by spiral similarity at
by spiral similarity at ![]() by some short angle chasing. Now, note that
by some short angle chasing. Now, note that ![]() is the altitude of
is the altitude of ![]() , as the altitude of
, as the altitude of ![]() . We need to compare these altitudes in order to compare their areas. Note that Stewart's theorem implies that
. We need to compare these altitudes in order to compare their areas. Note that Stewart's theorem implies that ![]() , the altitude of
, the altitude of ![]() . Similarly, the altitude of
. Similarly, the altitude of ![]() is the altitude of
is the altitude of ![]() , or
, or ![]() . However, it's not too hard to see that
. However, it's not too hard to see that ![]() , and therefore
, and therefore ![]() . From here, we get that the area of
. From here, we get that the area of ![]() is
is ![]() , by similarity. ~awang11
, by similarity. ~awang11
Solution 2(coord bash + basic geometry)
Let ![]() lie on the x-axis and
lie on the x-axis and ![]() be the origin.
be the origin. ![]() is
is ![]() . Use Heron's formula to compute the area of triangle
. Use Heron's formula to compute the area of triangle ![]() . We have
. We have ![]() . and
. and ![]() . We now find the altitude, which is
. We now find the altitude, which is ![]() , which is the y-coordinate of
, which is the y-coordinate of ![]() . We now find the x-coordinate of
. We now find the x-coordinate of ![]() , which satisfies
, which satisfies ![]() , which gives
, which gives ![]() since the triangle is acute. Now using the Angle Bisector Theorem, we have
since the triangle is acute. Now using the Angle Bisector Theorem, we have ![]() and
and ![]() to get
to get ![]() . The coordinates of D are
. The coordinates of D are ![]() . Since we want the area of triangle
. Since we want the area of triangle ![]() , we will find equations for perpendicular bisector of AD, and the other two angle bisectors. The perpendicular bisector is not too challenging: the midpoint of AD is
, we will find equations for perpendicular bisector of AD, and the other two angle bisectors. The perpendicular bisector is not too challenging: the midpoint of AD is ![]() and the slope of AD is
and the slope of AD is ![]() . The slope of the perpendicular bisector is
. The slope of the perpendicular bisector is ![]() . The equation is(in point slope form)
. The equation is(in point slope form) ![]() . The slope of AB, or in trig words, the tangent of
. The slope of AB, or in trig words, the tangent of ![]() is
is ![]() . Finding
. Finding ![]() and
and ![]() . Plugging this in to half angle tangent, it gives
. Plugging this in to half angle tangent, it gives  as the slope of the angle bisector, since it passes through
as the slope of the angle bisector, since it passes through ![]() , the equation is
, the equation is ![]() . Similarly, the equation for the angle bisector of
. Similarly, the equation for the angle bisector of ![]() will be
will be ![]() . For
. For ![]() use the B-angle bisector and the perpendicular bisector of AD equations to intersect at
use the B-angle bisector and the perpendicular bisector of AD equations to intersect at ![]() . For
. For ![]() use the C-angle bisector and the perpendicular bisector of AD equations to intersect at
use the C-angle bisector and the perpendicular bisector of AD equations to intersect at ![]() . The area of AEF is equal to
. The area of AEF is equal to ![]() since AD is the altitude of that triangle with EF as the base, with
since AD is the altitude of that triangle with EF as the base, with ![]() being the height.
being the height. ![]() and
and ![]() , so
, so ![]() which gives
which gives ![]() . NEVER overlook coordinate bash in combination with beginner synthetic techniques.~vvluo
. NEVER overlook coordinate bash in combination with beginner synthetic techniques.~vvluo
Solution 3 (Coordinate Bash + Trig)
![[asy] size(8cm); defaultpen(fontsize(10pt)); pair A,B,C,I,D,M,T,Y,Z,EE,F; A=(0,3sqrt(7)); B=(-1,0); C=(9,0); I=incenter(A,B,C); D=extension(A,I,B,C); M=(A+D)/2; draw(B--EE,gray+dashed); draw(C--F,gray+dashed); draw(A--B--C--A); draw(A--D); draw(B--(5,sqrt(28))); draw(M--(5,sqrt(28))); draw(C--(0,9sqrt(7)/7)); draw(M--(0,9sqrt(7)/7)); dot("$A$",A,NW); dot("$B$",B,SW); dot("$C$",C,SE); dot("$D$",D,S); dot("$E$",(5,sqrt(28)),N); dot("$M$",M,dir(70)); dot("$F$",(0,9sqrt(7)/7),N); label("$2$",B--D,S); label("$3$",D--C,S); label("$6$",A--C,N); label("$4$",A--B,W); [/asy]](https://latex.artofproblemsolving.com/d/4/3/d43487e9c27f6ed2a883159b67ebf63c992d7c1e.png)
Let ![]() and
and ![]() be the line
be the line ![]() . We compute that
. We compute that ![]() , so
, so ![]() . Thus,
. Thus, ![]() lies on the line
lies on the line ![]() . The length of
. The length of ![]() at a point
at a point ![]() is
is ![]() , so
, so ![]() .
.
We now have the coordinates  ,
, ![]() and
and ![]() . We also have
. We also have ![]() by the angle-bisector theorem and
by the angle-bisector theorem and  by taking the midpoint. We have that because
by taking the midpoint. We have that because ![]() ,
, ![]() by half angle formula.
by half angle formula.
We also compute ![]() , so
, so ![]() .
.
Now, ![]() has slope
has slope  , so it's perpendicular bisector has slope
, so it's perpendicular bisector has slope ![]() and goes through
and goes through  .
.
We find that this line has equation ![]() .
.
As ![]() , we have that line
, we have that line ![]() has form
has form ![]() . Solving for the intersection point of these two lines, we get
. Solving for the intersection point of these two lines, we get ![]() and thus
and thus ![]()
We also have that because ![]() ,
, ![]() has form
has form ![]() .
.
Intersecting the line ![]() and the perpendicular bisector of
and the perpendicular bisector of ![]() yields
yields ![]() .
.
Solving this, we get ![]() and so
and so  .
.
We now compute  . We also have
. We also have  .
.
As ![]() , we have
, we have ![$[\triangle{AEF}]=\frac{1}{2}\left(\frac{3\sqrt{2}}{2}\times\frac{5\sqrt{14}}{7}\right)=\frac{15\sqrt{7}}{14}$](https://latex.artofproblemsolving.com/c/4/f/c4fd18cdbe768738f8d5fa899470d7d7f0d2d899.png) .
.
The desired answer is ![]() ~Imayormaynotknowcalculus
~Imayormaynotknowcalculus
Solution 4 (Barycentric Coordinates)
![[asy] size(8cm); defaultpen(fontsize(10pt)); pair A,B,C,I,D,M,T,Y,Z,EE,F; A=(0,3sqrt(7)); B=(-1,0); C=(9,0); I=incenter(A,B,C); D=extension(A,I,B,C); M=(A+D)/2; draw(B--EE,gray+dashed); draw(C--F,gray+dashed); draw(A--B--C--A); draw(A--D); draw(B--(5,sqrt(28))); draw(M--(5,sqrt(28))); draw(C--(0,9sqrt(7)/7)); draw(M--(0,9sqrt(7)/7)); dot("$A$",A,NW); dot("$B$",B,SW); dot("$C$",C,SE); dot("$D$",D,S); dot("$E$",(5,sqrt(28)),N); dot("$M$",M,dir(70)); dot("$F$",(0,9sqrt(7)/7),N); label("$2$",B--D,S); label("$3$",D--C,S); label("$6$",A--C,N); label("$4$",A--B,W); [/asy]](https://latex.artofproblemsolving.com/d/4/3/d43487e9c27f6ed2a883159b67ebf63c992d7c1e.png)
As usual, we will use homogenized barycentric coordinates.
We have that ![]() will have form
will have form ![]() . Similarly,
. Similarly, ![]() has form
has form ![]() and
and ![]() has form
has form ![]() . Since
. Since ![]() and
and ![]() , we also have
, we also have ![]() . It remains to determine the equation of the line formed by the perpendicular bisector of
. It remains to determine the equation of the line formed by the perpendicular bisector of ![]() .
.
This can be found using EFFT. Let a point ![]() on
on ![]() have coordinates
have coordinates ![]() . We then have that the displacement vector
. We then have that the displacement vector ![]() and that the displacement vector
and that the displacement vector ![]() has form
has form ![]() . Now, by EFFT, we have
. Now, by EFFT, we have ![]() . This equates to
. This equates to ![]() .
.
Now, intersecting this with ![]() , we have
, we have ![]() ,
, ![]() , and
, and ![]() . This yields
. This yields ![]() ,
, ![]() , and
, and ![]() , or
, or ![]() .
.
Similarly, intersecting this with ![]() , we have
, we have ![]() ,
, ![]() , and
, and ![]() . Solving this, we obtain
. Solving this, we obtain ![]() ,
, ![]() , and
, and ![]() , or
, or ![]() .
.
We finish by invoking the Barycentric Distance Formula twice; our first displacement vector being ![]() . We then have
. We then have ![]() , thus
, thus ![]() .
.
Our second displacement vector is ![]() . As a result,
. As a result, ![]() , so
, so ![]() .
.
As ![]() , the desired area is
, the desired area is ![]() . ~Imayormaynotknowcalculus
. ~Imayormaynotknowcalculus
Remark: The area of ![]() can also be computed using the Barycentric Area Formula, although it may increase the risk of computational errors; there are also many different ways to proceed once the coordinates are determined.
can also be computed using the Barycentric Area Formula, although it may increase the risk of computational errors; there are also many different ways to proceed once the coordinates are determined.
Solution 5 (geometry+trig)
![[asy] size(8cm); defaultpen(fontsize(10pt)); pair A,B,C,I,D,M,T,Y,Z,EE,F; A=(0,3sqrt(7)); B=(-1,0); C=(9,0); I=incenter(A,B,C); D=extension(A,I,B,C); M=(A+D)/2; draw(B--EE,gray+dashed); draw(C--F,gray+dashed); draw(A--B--C--A); draw(A--D); draw(A--(5,sqrt(28))); draw(A--(0,9sqrt(7)/7)); draw(D--(0,9sqrt(7)/7)); draw(D--(5,sqrt(28))); draw(B--(5,sqrt(28))); draw(M--(5,sqrt(28))); draw(C--(0,9sqrt(7)/7)); draw(M--(0,9sqrt(7)/7)); dot("$A$",A,NW); dot("$B$",B,SW); dot("$C$",C,SE); dot("$D$",D,S); dot("$E$",(5,sqrt(28)),N); dot("$M$",M,dir(70)); dot("$F$",(0,9sqrt(7)/7),N); label("$2$",B--D,S); label("$3$",D--C,S); label("$6$",A--C,N); label("$4$",A--B,W); [/asy]](https://latex.artofproblemsolving.com/7/9/6/796ab03dc5983033934843648e06565cc3ee3ac8.png)
To get the area of ![]() , we try to find
, we try to find ![]() and
and ![]() .
.
Since ![]() is the angle bisector, we can get that
is the angle bisector, we can get that ![]() and
and ![]() . By applying Stewart's Theorem, we can get that
. By applying Stewart's Theorem, we can get that ![]() . Therefore
. Therefore ![]() .
.
Since ![]() is the perpendicular bisector of
is the perpendicular bisector of ![]() , we know that
, we know that ![]() . Since
. Since ![]() is the angle bisector of
is the angle bisector of ![]() , we know that
, we know that ![]() . By applying the Law of Sines to
. By applying the Law of Sines to ![]() and
and ![]() , we know that
, we know that ![]() . Since
. Since ![]() is not equal to
is not equal to ![]() and therefore these two triangles are not congruent, we know that
and therefore these two triangles are not congruent, we know that ![]() and
and ![]() are supplementary. Then we know that
are supplementary. Then we know that ![]() and
and ![]() are also supplementary. Given that
are also supplementary. Given that ![]() , we can get that
, we can get that ![]() is half of
is half of ![]() . Similarly, we have
. Similarly, we have ![]() is half of
is half of ![]() .
.
By applying the Law of Cosines, we get ![]() , and then
, and then ![]() . Similarly, we can get
. Similarly, we can get ![]() and
and ![]() . Based on some trig identities, we can compute that
. Based on some trig identities, we can compute that ![]() , and
, and ![]() .
.
Finally, the area of ![]() equals
equals ![]() . Therefore, the final answer is
. Therefore, the final answer is ![]() . ~xamydad
. ~xamydad
Remark: I didn't figure out how to add segments ![]() ,
, ![]() ,
, ![]() and
and ![]() . Can someone please help add these segments?
. Can someone please help add these segments?
(Added 🙂 ~Math_Genius_164)
Solution 6
First and foremost ![]() as
as ![]() is the perpendicular bisector of
is the perpendicular bisector of ![]() . Now note that quadrilateral
. Now note that quadrilateral ![]() is cyclic, because
is cyclic, because ![]() and
and ![]() . Similarly quadrilateral
. Similarly quadrilateral ![]() is cyclic,
is cyclic,![]() Let
Let ![]() ,
,![]() ,
, ![]() be the
be the ![]() ,
,![]() , and
, and ![]() excenters of
excenters of ![]() respectively. Then it follows that
respectively. Then it follows that ![]() . By angle bisector theorem we have
. By angle bisector theorem we have ![]() . Now let the feet of the perpendiculars from
. Now let the feet of the perpendiculars from ![]() and
and ![]() to
to ![]() be
be ![]() and
and ![]() resptively. Then by tangents we have
resptively. Then by tangents we have![]()
![]() From the previous ratios,
From the previous ratios, ![]() Similarly we can find that
Similarly we can find that ![]() and
and ![]() and thus
and thus![]() -tkhalid
-tkhalid
14.Solution 1
Either ![]() or not. We first see that if
or not. We first see that if ![]() it's easy to obtain by Vieta's that
it's easy to obtain by Vieta's that ![]() . Now, take
. Now, take ![]() and WLOG
and WLOG ![]() . Now, consider the parabola formed by the graph of
. Now, consider the parabola formed by the graph of ![]() . It has vertex
. It has vertex ![]() . Now, say that
. Now, say that ![]() . We note
. We note ![]() . Now, we note
. Now, we note ![]() by plugging in again. Now, it's easy to find that
by plugging in again. Now, it's easy to find that ![]() , yielding a value of
, yielding a value of ![]() . Finally, we add
. Finally, we add ![]() . ~awang11, charmander3333
. ~awang11, charmander3333
Remark: We know that ![]() from
from ![]() .
.
Solution 2
Let the roots of ![]() be
be ![]() and
and ![]() , then we can write
, then we can write ![]() . The fact that
. The fact that ![]() has solutions
has solutions ![]() implies that some combination of
implies that some combination of ![]() of these are the solution to
of these are the solution to ![]() , and the other
, and the other ![]() are the solution to
are the solution to ![]() . It's fairly easy to see there are only
. It's fairly easy to see there are only ![]() possible such groupings:
possible such groupings: ![]() and
and ![]() , or
, or ![]() and
and ![]() (Note that
(Note that ![]() are interchangeable, and so are
are interchangeable, and so are ![]() and
and ![]() ). We now casework: If
). We now casework: If ![]() , then
, then![]()
![]() so this gives
so this gives ![]() . Next, if
. Next, if ![]() , then
, then![]()
![]() Subtracting the first part of the first equation from the first part of the second equation gives
Subtracting the first part of the first equation from the first part of the second equation gives![]() Hence,
Hence, ![]() , and so
, and so ![]() . Therefore, the solution is
. Therefore, the solution is ![]() ~ktong
~ktong
Solution 3
Write ![]() . Split the problem into two cases:
. Split the problem into two cases: ![]() and
and ![]() .
.
Case 1: We have ![]() . We must have
. We must have![]() Rearrange and divide through by
Rearrange and divide through by ![]() to obtain
to obtain![]() Now, note that
Now, note that![]()
![]() Now, rearrange to get
Now, rearrange to get![]() and thus
and thus![]() Substituting this into our equation for
Substituting this into our equation for ![]() yields
yields ![]() . Then, it is clear that
. Then, it is clear that ![]() does not have a double root at
does not have a double root at ![]() , so we must have
, so we must have ![]() and
and ![]() or vice versa. This gives
or vice versa. This gives ![]() and
and ![]() or vice versa, implying that
or vice versa, implying that ![]() and
and ![]() .
.
Case 2: We have ![]() . Then, we must have
. Then, we must have ![]() . It is clear that
. It is clear that ![]() (we would otherwise get
(we would otherwise get ![]() implying
implying ![]() or vice versa), so
or vice versa), so ![]() and
and ![]() .
.
Thus, our final answer is ![]() . ~GeronimoStilton
. ~GeronimoStilton
Solution 4
Let ![]() . There are two cases: in the first case,
. There are two cases: in the first case, ![]() equals
equals ![]() (without loss of generality), and thus
(without loss of generality), and thus ![]() . By Vieta's formulas
. By Vieta's formulas ![]() .
.
In the second case, say without loss of generality ![]() and
and ![]() . Subtracting gives
. Subtracting gives ![]() , so
, so ![]() . From this, we have
. From this, we have ![]() .
.
Note ![]() , so by Vieta's, we have
, so by Vieta's, we have ![]() . In this case,
. In this case, ![]() .
.
The requested sum is ![]() .~TheUltimate123
.~TheUltimate123
15.Solution 1
The following is a power of a point solution to this menace of a problem:![[asy] /* Geogebra to Asymptote conversion, documentation at artofproblemsolving.com/Wiki go to User:Azjps/geogebra */ import graph; size(18cm); real labelscalefactor = 0.5; /* changes label-to-point distance */ pen dps = linewidth(0.7) + fontsize(10); defaultpen(dps); /* default pen style */ pen dotstyle = black; /* point style */ real xmin = -12.821705655137235, xmax = 10.870448356581754, ymin = -3.0673360097491003, ymax = 10.363346102088961; /* image dimensions */ pen wrwrwr = rgb(0.3803921568627451,0.3803921568627451,0.3803921568627451); /* draw figures */ draw((xmin, 0.0052470390246834855*xmin + 3.437118410441658)--(xmax, 0.0052470390246834855*xmax + 3.437118410441658), linewidth(2) + wrwrwr); /* line */ draw(circle((-4.538171990791266,4.905585481447388), 4.693275552848494), linewidth(2) + wrwrwr); draw(circle((-4.522512329243054,1.9211095752183682), 4.693275552848494), linewidth(2) + wrwrwr); draw((xmin, -190.58367877496823*xmin-1479.5139994609244)--(xmax, -190.58367877496823*xmax-1479.5139994609244), linewidth(2) + wrwrwr); /* line */ draw((xmin, 0.9703333412757664*xmin + 12.849035992754926)--(xmax, 0.9703333412757664*xmax + 12.849035992754926), linewidth(2) + wrwrwr); /* line */ draw(circle((-7.790821079477277,5.289342543424063), 1.8930768158550504), linewidth(2) + wrwrwr); draw((xmin, -1.0305736775830343*xmin-5.438100054565965)--(xmax, -1.0305736775830343*xmax-5.438100054565965), linewidth(2) + wrwrwr); /* line */ draw((xmin, -1.0305736775830343*xmin + 0.22866488339331612)--(xmax, -1.0305736775830343*xmax + 0.22866488339331612), linewidth(2) + wrwrwr); /* line */ /* dots and labels */ dot((-8.98,3.39),dotstyle); label("$B$", (-8.914038694762803,3.548005694821766), NE * labelscalefactor); dot((-0.08068432003432058,3.4366950566657577),dotstyle); label("$C$", (-0.021788682572170717,3.594159241597842), NE * labelscalefactor); dot((-4.538171990791266,4.905585481447388),dotstyle); label("$O$", (-4.483298204259513,5.055688222840243), NE * labelscalefactor); dot((-4.522512329243054,1.9211095752183682),linewidth(4pt) + dotstyle); label("$O'$", (-4.467913688667488,2.0403231668032897), NE * labelscalefactor); dot((-7.790821079477277,5.289342543424063),dotstyle); label("$H$", (-7.729430994176854,5.440301112640874), NE * labelscalefactor); dot((-7.806480741025488,8.273818449653083),linewidth(4pt) + dotstyle); label("$A$", (-7.7448155097688804,8.394128106309726), NE * labelscalefactor); dot((-9.139423209055858,3.980748932978468),linewidth(4pt) + dotstyle); label("$X$", (-9.083268366275083,4.101848256134676), NE * labelscalefactor); dot((-9.752410287411378,3.3859471330788855),linewidth(4pt) + dotstyle); label("$K$", (-9.68326447436407,3.5018521480456903), NE * labelscalefactor); dot((-3.475227037470366,9.476907329794422),linewidth(4pt) + dotstyle); label("$Y$", (-3.4063821128177407,9.594120322487697), NE * labelscalefactor); dot((-7.780888168280388,3.3962917865759925),linewidth(4pt) + dotstyle); label("$L$", (-7.714046478584829,3.5172366636377155), NE * labelscalefactor); dot((-7.776585346090923,2.5762441045932913),linewidth(4pt) + dotstyle); label("$D$", (-7.714046478584829,2.7018573372603765), NE * labelscalefactor); dot((-6.307325123263112,6.728828131386446),linewidth(4pt) + dotstyle); label("$E$", (-6.252517497342424,6.855676547107199), NE * labelscalefactor); clip((xmin,ymin)--(xmin,ymax)--(xmax,ymax)--(xmax,ymin)--cycle); /* end of picture */ [/asy]](https://latex.artofproblemsolving.com/c/6/9/c69347dc6d83100199168eca216342c5fd324419.png)
Let points be what they appear as in the diagram below. Note that ![]() is not insignificant; from here, we set
is not insignificant; from here, we set ![]() by PoP and trivial construction. Now,
by PoP and trivial construction. Now, ![]() is the reflection of
is the reflection of ![]() over
over ![]() . Note
. Note ![]() , and therefore by Pythagorean theorem we have
, and therefore by Pythagorean theorem we have ![]() . Consider
. Consider ![]() . We have that
. We have that ![]() , and therefore we are ready to PoP with respect to
, and therefore we are ready to PoP with respect to ![]() . Setting
. Setting ![]() , we obtain
, we obtain ![]() by PoP on
by PoP on ![]() , and furthermore, we have
, and furthermore, we have ![]() . Now, we get
. Now, we get ![]() , and from
, and from ![]() we take
we take![]() However, squaring and manipulating with
However, squaring and manipulating with ![]() yields that
yields that ![]() and from here, since
and from here, since ![]() we get the area to be
we get the area to be ![]() . ~awang11's sol
. ~awang11's sol
Solution 1a
As in the diagram, let ray ![]() extended hits BC at L and the circumcircle at say
extended hits BC at L and the circumcircle at say ![]() . By power of the point at H, we have
. By power of the point at H, we have ![]() . The three values we are given tells us that
. The three values we are given tells us that ![]() . L is the midpoint of
. L is the midpoint of ![]() (see here: https://www.cut-the-knot.org/Curriculum/Geometry/AltitudeAndCircumcircle.shtml ), so
(see here: https://www.cut-the-knot.org/Curriculum/Geometry/AltitudeAndCircumcircle.shtml ), so ![]() .
.
As in the diagram provided, let K be the intersection of ![]() and
and ![]() . By power of a point on the circumcircle of triangle
. By power of a point on the circumcircle of triangle ![]() ,
, ![]() . By power of a point on the circumcircle of triangle
. By power of a point on the circumcircle of triangle ![]() ,
, ![]() , thus
, thus ![]() . Solving gives
. Solving gives ![]() or
or ![]() .
.
By the Pythagorean Theorem on triangle ![]() ,
, ![]() . Now continue with solution 1.
. Now continue with solution 1.
Solution 2
![[asy] size(10cm); pair A, B, C, D, H, K, O, P, L, M, X, Y; A = (-15, 27); B = (-24, 0); C = (24, 0); D = (-8.28, 18.04); O = (0, 7); P = (0, -7); H = (-15, 13); K = (-15, -13); M = (0, 0); L = (-15, 0); X = (-24.9569, 5.53234); Y = (8.39688, 30.5477); draw(circle(O, 25)); draw(circle(P, 25)); draw(A--B--C--cycle); draw(H -- K); draw(A -- O -- P -- H -- cycle); draw(X -- Y); draw(O -- X, dashed); draw(O -- Y, dashed); draw(O -- B, dashed); draw(O -- C, dashed); label("$O$", O, ENE); label("$A$", A, NW); label("$B$", B, W); label("$C$", C, E); label("$H$", H, E); label("$H'$", K, NE); label("$X$", X, W); label("$Y$", Y, NE); label("$O'$", P, E); label("$M$", M, NE); label("$L$", L, NE); label("$D$", D, NNE); label("$2$", X -- H, NW); label("$3$", H -- A, SW); label("$6$", H -- Y, NW); label("$R$", O -- Y, E); dot(O); dot(P); dot(D); dot(H); [/asy]](https://latex.artofproblemsolving.com/9/3/c/93cbdb7042dcdfd8bcc8debd055e6439bd394e78.png) Diagram not to scale.
Diagram not to scale.
We first observe that ![]() , the image of the reflection of
, the image of the reflection of ![]() over line
over line ![]() , lies on circle
, lies on circle ![]() . This is because
. This is because ![]() . This is a well known lemma. The result of this observation is that circle
. This is a well known lemma. The result of this observation is that circle ![]() , the circumcircle of
, the circumcircle of ![]() is the image of circle
is the image of circle ![]() over line
over line ![]() , which in turn implies that
, which in turn implies that ![]() and thus
and thus ![]() is a parallelogram. That
is a parallelogram. That ![]() is a parallelogram implies that
is a parallelogram implies that ![]() is perpendicular to
is perpendicular to ![]() , and thus divides segment
, and thus divides segment ![]() in two equal pieces,
in two equal pieces, ![]() and
and ![]() , of length
, of length ![]() .
.
Using Power of a Point,![]() This means that
This means that ![]() and
and ![]() , where
, where ![]() is the foot of the altitude from
is the foot of the altitude from ![]() onto
onto ![]() . All that remains to be found is the length of segment
. All that remains to be found is the length of segment ![]() .
.
Looking at right triangle ![]() , we find that
, we find that![]() Looking at right triangle
Looking at right triangle ![]() , we get the equation
, we get the equation![]() Plugging in known values, and letting
Plugging in known values, and letting ![]() be the radius of the circle, we find that
be the radius of the circle, we find that![]()
Recall that ![]() is a parallelogram, so
is a parallelogram, so ![]() . So,
. So, ![]() , where
, where ![]() is the midpoint of
is the midpoint of ![]() . This means that
. This means that![\[\overline{BC} = 2\overline{BM} = 2\sqrt{R^2 - \left(\frac32\right)^2} = 2\sqrt{\frac{441}{20} - \frac{9}{4}} = \frac{6\sqrt{55}}{5}\]](https://latex.artofproblemsolving.com/5/c/1/5c1a7e3b7fbbbe6efb52c90e25dc8993d9f7ce7c.png)
Thus, the area of triangle ![]() is
is![]() The answer is
The answer is ![]() .
.
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1