- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
2003AMC10B真题与答案解析
2003AMC10B真题
真题及解析
Problem 1
Which of the following is the same as
![]()
![]()
Problem 2
Al gets the disease algebritis and must take one green pill and one pink pill each day for two weeks. A green pill costs ![]()
![]() more than a pink pill, and Al's pills cost a total of
more than a pink pill, and Al's pills cost a total of ![]()
![]() for the two weeks. How much does one green pill cost?
for the two weeks. How much does one green pill cost?
![]()
![]()
![]()
![]()
![]()
![]()
Problem 3
The sum of ![]() consecutive even integers is
consecutive even integers is ![]() less than the sum of the first
less than the sum of the first ![]() consecutive odd counting numbers. What is the smallest of the even integers?
consecutive odd counting numbers. What is the smallest of the even integers?
![]()
Problem 4
Rose fills each of the rectangular regions of her rectangular flower bed with a different type of flower. The lengths, in feet, of the rectangular regions in her flower bed are as shown in the figure. She plants one flower per square foot in each region. Asters cost ![]()
![]() each, begonias
each, begonias ![]()
![]() each, cannas
each, cannas ![]()
![]() each, dahlias
each, dahlias ![]()
![]() each, and Easter lilies
each, and Easter lilies ![]()
![]() each. What is the least possible cost, in dollars, for her garden?
each. What is the least possible cost, in dollars, for her garden?
![[asy] unitsize(5mm); defaultpen(linewidth(.8pt)+fontsize(8pt)); draw((6,0)--(0,0)--(0,1)--(6,1)); draw((0,1)--(0,6)--(4,6)--(4,1)); draw((4,6)--(11,6)--(11,3)--(4,3)); draw((11,3)--(11,0)--(6,0)--(6,3)); label("1",(0,0.5),W); label("5",(0,3.5),W); label("3",(11,1.5),E); label("3",(11,4.5),E); label("4",(2,6),N); label("7",(7.5,6),N); label("6",(3,0),S); label("5",(8.5,0),S);[/asy]](https://latex.artofproblemsolving.com/5/3/6/53688e514d1c6f1f99b771578717677d9fec99b3.png)
![]()
Problem 5
Moe uses a mower to cut his rectangular ![]() -foot by
-foot by ![]() -foot lawn. The swath he cuts is
-foot lawn. The swath he cuts is ![]() inches wide, but he overlaps each cut by
inches wide, but he overlaps each cut by ![]() inches to make sure that no grass is missed. He walks at the rate of
inches to make sure that no grass is missed. He walks at the rate of ![]() feet per hour while pushing the mower. Which of the following is closest to the number of hours it will take Moe to mow the lawn?
feet per hour while pushing the mower. Which of the following is closest to the number of hours it will take Moe to mow the lawn?
![]()
Problem 6
Many television screens are rectangles that are measured by the length of their diagonals. The ratio of the horizontal length to the height in a standard television screen is ![]() . The horizontal length of a "
. The horizontal length of a "![]() -inch" television screen is closest, in inches, to which of the following?
-inch" television screen is closest, in inches, to which of the following?
![[asy] import math; unitsize(7mm); defaultpen(linewidth(.8pt)+fontsize(8pt)); draw((0,0)--(4,0)--(4,3)--(0,3)--(0,0)--(4,3)); fill((0,0)--(4,0)--(4,3)--cycle,mediumgray); label(rotate(aTan(3.0/4.0))*"Diagonal",(2,1.5),NW); label(rotate(90)*"Height",(4,1.5),E); label("Length",(2,0),S);[/asy]](https://latex.artofproblemsolving.com/8/d/a/8da5bd50273e6772bc01914af3e7e60effc287b9.png)
![]()
Problem 7
The symbolism ![]() denotes the largest integer not exceeding
denotes the largest integer not exceeding ![]() . For example,
. For example, ![]() and
and ![]() . Compute
. Compute![]()
![]()
Problem 8
The second and fourth terms of a geometric sequence are ![]() and
and ![]() . Which of the following is a possible first term?
. Which of the following is a possible first term?
![]()
Problem 9
Find the value of ![]() that satisfies the equation
that satisfies the equation![]()
![]()
Problem 10
Nebraska, the home of the AMC, changed its license plate scheme. Each old license plate consisted of a letter followed by four digits. Each new license plate consists of the three letters followed by three digits. By how many times is the number of possible license plates increased?
![]()
Problem 11
A line with slope ![]() intersects a line with slope
intersects a line with slope ![]() at point
at point ![]() . What is the distance between the
. What is the distance between the ![]() -intercepts of these two lines?
-intercepts of these two lines?
![]()
Problem 12
Al, Betty, and Clare split ![]()
![]() among them to be invested in different ways. Each begins with a different amount. At the end of one year, they have a total of
among them to be invested in different ways. Each begins with a different amount. At the end of one year, they have a total of ![]()
![]() . Betty and Clare have both doubled their money, whereas Al has managed to lose
. Betty and Clare have both doubled their money, whereas Al has managed to lose ![]()
![]() . What was Al's original portion?
. What was Al's original portion?
![]()
![]()
![]()
![]()
![]()
![]()
Problem 13
Let ![]() denote the sum of the digits of the positive integer
denote the sum of the digits of the positive integer ![]() . For example,
. For example, ![]() and
and ![]() . For how many two-digit values of
. For how many two-digit values of ![]() is
is ![]() ?
?
![]()
Problem 14
Given that ![]() where both
where both ![]() and
and ![]() are positive integers, find the smallest possible value for
are positive integers, find the smallest possible value for ![]() .
.
![]()
Problem 15
There are ![]() players in a single tennis tournament. The tournament is single elimination, meaning that a player who loses a match is eliminated. In the first round, the strongest
players in a single tennis tournament. The tournament is single elimination, meaning that a player who loses a match is eliminated. In the first round, the strongest ![]() players are given a bye, and the remaining
players are given a bye, and the remaining ![]() players are paired off to play. After each round, the remaining players play in the next round. The tournament continues until only one player remains unbeaten. The total number of matches played is
players are paired off to play. After each round, the remaining players play in the next round. The tournament continues until only one player remains unbeaten. The total number of matches played is
![]()
Problem 16
A restaurant offers three desserts, and exactly twice as many appetizers as main courses. A dinner consists of an appetizer, a main course, and a dessert. What is the least number of main courses that a restaurant should offer so that a customer could have a different dinner each night in the year ![]() ?
?
![]()
Problem 17
An ice cream cone consists of a sphere of vanilla ice cream and a right circular cone that has the same diameter as the sphere. If the ice cream melts, it will exactly fill the cone. Assume that the melted ice cream occupies ![]() of the volume of the frozen ice cream. What is the ratio of the cone's height to its radius? (Note: a cone with radius
of the volume of the frozen ice cream. What is the ratio of the cone's height to its radius? (Note: a cone with radius ![]() and height
and height ![]() has volume
has volume ![]() and a sphere with radius
and a sphere with radius ![]() has volume
has volume ![]() .)
.)
![]()
Problem 18
What is the largest integer that is a divisor of![]() for all positive even integers
for all positive even integers ![]() ?
?
![]()
Problem 19
Three semicircles of radius ![]() are constructed on diameter
are constructed on diameter ![]() of a semicircle of radius
of a semicircle of radius ![]() . The centers of the small semicircles divide
. The centers of the small semicircles divide ![]() into four line segments of equal length, as shown. What is the area of the shaded region that lies within the large semicircle but outside the smaller semicircles?
into four line segments of equal length, as shown. What is the area of the shaded region that lies within the large semicircle but outside the smaller semicircles?
![[asy] import graph; unitsize(14mm); defaultpen(linewidth(.8pt)+fontsize(8pt)); dashed=linetype("4 4"); dotfactor=3; pair A=(-2,0), B=(2,0); fill(Arc((0,0),2,0,180)--cycle,mediumgray); fill(Arc((-1,0),1,0,180)--cycle,white); fill(Arc((0,0),1,0,180)--cycle,white); fill(Arc((1,0),1,0,180)--cycle,white); draw(Arc((-1,0),1,60,180)); draw(Arc((0,0),1,0,60),dashed); draw(Arc((0,0),1,60,120)); draw(Arc((0,0),1,120,180),dashed); draw(Arc((1,0),1,0,120)); draw(Arc((0,0),2,0,180)--cycle); dot((0,0)); dot((-1,0)); dot((1,0)); draw((-2,-0.1)--(-2,-0.3),gray); draw((-1,-0.1)--(-1,-0.3),gray); draw((1,-0.1)--(1,-0.3),gray); draw((2,-0.1)--(2,-0.3),gray); label("$A$",A,W); label("$B$",B,E); label("1",(-1.5,-0.1),S); label("2",(0,-0.1),S); label("1",(1.5,-0.1),S);[/asy]](https://latex.artofproblemsolving.com/b/c/6/bc697df5c9078d8ccf0708f353185c707d3275d4.png)
![]()
Problem 20
In rectangle ![]() and
and ![]() . Points
. Points ![]() and
and ![]() are on
are on ![]() so that
so that ![]() and
and ![]() . Lines
. Lines ![]() and
and ![]() intersect at
intersect at ![]() . Find the area of
. Find the area of ![]() .
.
![[asy] unitsize(6mm); defaultpen(linewidth(.8pt)+fontsize(8pt)); pair A=(0,0), B=(5,0), C=(5,3), D=(0,3), F=(1,3), G=(3,3); pair E=extension(A,F,B,G); draw(A--B--C--D--A--E--B); label("$A$",A,SW); label("$B$",B,SE); label("$C$",C,NE); label("$D$",D,NW); label("$E$",E,N); label("$F$",F,SE); label("$G$",G,SW); label("$B$",B,SE); label("1",midpoint(D--F),N); label("2",midpoint(G--C),N); label("3",midpoint(B--C),E); label("3",midpoint(A--D),W); label("5",midpoint(A--B),S); [/asy]](https://latex.artofproblemsolving.com/6/5/0/650503cba159d88cab849aafb4c441606631685b.png)
![]()
Problem 21
A bag contains two red beads and two green beads. You reach into the bag and pull out a bead, replacing it with a red bead regardless of the color you pulled out. What is the probability that all beads in the bag are red after three such replacements?
![]()
Problem 22
A clock chimes once at ![]() minutes past each hour and chimes on the hour according to the hour. For example, at
minutes past each hour and chimes on the hour according to the hour. For example, at ![]() there is one chime and at noon and midnight there are twelve chimes. Starting at
there is one chime and at noon and midnight there are twelve chimes. Starting at ![]() on
on ![]() on what date will the
on what date will the ![]() chime occur?
chime occur?
![]()
Problem 23
A regular octagon ![]() has an area of one square unit. What is the area of the rectangle
has an area of one square unit. What is the area of the rectangle ![]() ?
?
![[asy] unitsize(10mm); defaultpen(linewidth(.8pt)+fontsize(8pt)); pair C=dir(22.5), B=dir(67.5), A=dir(112.5), H=dir(157.5), G=dir(202.5), F=dir(247.5), E=dir(292.5), D=dir(337.5); draw(A--B--C--D--E--F--G--H--cycle); label("$A$",A,NNW); label("$B$",B,NNE); label("$C$",C,ENE); label("$D$",D,ESE); label("$E$",E,SSE); label("$F$",F,SSW); label("$G$",G,WSW); label("$H$",H,WNW); [/asy]](https://latex.artofproblemsolving.com/2/6/c/26c888f252889265fb2d2ba34db0e8a48c55c6d4.png)
![]()
Problem 24
The first four terms in an arithmetic sequence are ![]() and
and ![]() in that order. What is the fifth term?
in that order. What is the fifth term?
![]()
Problem 25
How many distinct four-digit numbers are divisible by ![]() and have
and have ![]() as their last two digits?
as their last two digits?
![]()
2003AMC10B详细解析
- The numbers in the numerator and denominator can be grouped like this:
 Alternatively, notice that each term in the numerator is
Alternatively, notice that each term in the numerator is  of a term in the denominator, so the quotient has to be
of a term in the denominator, so the quotient has to be  .
. - Because there are
 days in two weeks, Al spends
days in two weeks, Al spends  dollars per day for the cost of a green pill and a pink pill. If the green pill costs
dollars per day for the cost of a green pill and a pink pill. If the green pill costs  dollars and the pink pill
dollars and the pink pill  dollars, the sum of the two costs
dollars, the sum of the two costs  should equal
should equal  dollars. Then the cost of the green pill
dollars. Then the cost of the green pill  is
is  .
. - It is a well-known fact that the sum of the first
 odd numbers is
odd numbers is  . This makes the sum of the first
. This makes the sum of the first  odd numbers equal to
odd numbers equal to  .Let
.Let  be equal to the smallest of the
be equal to the smallest of the  even integers. Then
even integers. Then  is the next highest,
is the next highest,  even higher, and so on.This sets up the equation
even higher, and so on.This sets up the equation  Now we solve:
Now we solve:![[5n+24=64]](https://latex.artofproblemsolving.com/8/4/2/842502c8003c93ed53dca618860b689d6544279e.png)
![[5n=40]](https://latex.artofproblemsolving.com/d/e/3/de3e5e0f25b320e50496de28ad34bd574e697841.png)
![[n=8]](https://latex.artofproblemsolving.com/2/b/a/2ba83bf8758acefe099680e230795f472acecdae.png) Thus, the smallest integer is
Thus, the smallest integer is  .
. - The areas of the five regions from greatest to least are
 and
and  .If we want to minimize the cost, we want to maximize the area of the cheapest flower and minimize the area of the most expensive flower. Doing this, the cost is
.If we want to minimize the cost, we want to maximize the area of the cheapest flower and minimize the area of the most expensive flower. Doing this, the cost is  , which simplifies to
, which simplifies to 
 . Therefore the answer is
. Therefore the answer is  .
. - Since the swath Moe actually mows is
 inches, or
inches, or  feet wide, he mows
feet wide, he mows  square feet in one hour. His lawn has an area of
square feet in one hour. His lawn has an area of  , so it will take Moe
, so it will take Moe  hours to finish mowing the lawn. Thus the answer is
hours to finish mowing the lawn. Thus the answer is  .
. - If you divide the television screen into two right triangles, the legs are in the ratio of
 , and we can let one leg be
, and we can let one leg be  and the other be
and the other be  . Then we can use the Pythagorean Theorem.
. Then we can use the Pythagorean Theorem. The horizontal length is
The horizontal length is  , which is closest to
, which is closest to  .One can realize that the diagonal, vertical, and horizontal lengths all make up a
.One can realize that the diagonal, vertical, and horizontal lengths all make up a  triangle. Therefore, the horizontal length, being the
triangle. Therefore, the horizontal length, being the  in the
in the  ratio, is simply
ratio, is simply  times the hypotenuse.
times the hypotenuse.  .
. - The first three values in the sum are equal to
 the next five equal to
the next five equal to  the next seven equal to
the next seven equal to  and the last one equal to
and the last one equal to  For example, since
For example, since  any square root of a number less than
any square root of a number less than  must be less than
must be less than  Sum them all together to get
Sum them all together to get![[3cdot1 + 5cdot2 + 7cdot3 + 1cdot4 = 3+10+21+4 = boxed{textbf{(B) } 38}]](https://latex.artofproblemsolving.com/c/f/f/cffbd6bff0dc51c1c4487240a68ffad24446e9b3.png)
- Let the first term be
 and the common difference be
and the common difference be  . Therefore,
. Therefore,![[ar=2 (1) qquad text{and} qquad ar^3=6 (2)]](https://latex.artofproblemsolving.com/d/6/d/d6da05e8becb6457c46753fab5b6c95676cb5de6.png) Dividing
Dividing  by
by  eliminates the
eliminates the  , yielding
, yielding  , so
, so  .Now, since
.Now, since  ,
,  , so
, so  .We therefore see that
.We therefore see that  is a possible first term.
is a possible first term. - Manipulate the powers of
 in order to get a clean expression.
in order to get a clean expression.![[frac{5^{frac{48}{x}}}{5^{frac{26}{x}} cdot 25^{frac{17}{x}}} = frac{5^{frac{48}{x}}}{5^{frac{26}{x}} cdot 5^{frac{34}{x}}} = 5^{frac{48}{x}-(frac{26}{x}+frac{34}{x})} = 5^{-frac{12}{x}}]](https://latex.artofproblemsolving.com/e/e/7/ee7b66e25c28807e2bfea090fc8f89c5d6b41aa2.png)
![[25^{-2} = (5^2)^{-2} = 5^{-4}]](https://latex.artofproblemsolving.com/5/c/d/5cdb1a2ed954ee8fda8aae01c8a9032b16e28bba.png)
![[5^{-4} = 5^{-frac{12}{x}}]](https://latex.artofproblemsolving.com/2/1/9/219e5f75112057ae2f3f02acf33d2ea76bc8581b.png) If two numbers are equal, and their bases are equal, then their exponents are equal as well. Set the two exponents equal to each other.
If two numbers are equal, and their bases are equal, then their exponents are equal as well. Set the two exponents equal to each other.
- There are
 letters and
letters and  digits. There were
digits. There were  old license plates. There are
old license plates. There are  new license plates. The number of license plates increased by
new license plates. The number of license plates increased by![[frac{26^3 cdot 10^3}{26 cdot 10^4} = boxed{textbf{(C) } frac{26^2}{10}}]](https://latex.artofproblemsolving.com/b/c/e/bce4220f1b7d53e103e486a9453b3f8368d28bf8.png)
- Using the point-slope form, the equation of each line is
![[y-15=3(x-10) longrightarrow y=3x-15]](https://latex.artofproblemsolving.com/4/b/0/4b037a952efd3a1d90f21cfae3201b8b27e6e249.png)
![[y-15=5(x-10) longrightarrow y=5x-35]](https://latex.artofproblemsolving.com/9/3/6/9363e785bc07ef6d3345ffff2b3cd345be5fdb2e.png) Substitute in
Substitute in  to find the
to find the  -intercepts.
-intercepts.![[0=3x-15longrightarrow x=5]](https://latex.artofproblemsolving.com/c/8/5/c85ab0e6b9308cb0549a47dac89e43636d46944a.png)
![[0=5x-35longrightarrow x=7]](https://latex.artofproblemsolving.com/7/d/9/7d97578c90c79935d44e9e03ca1693dce68b80d0.png) The difference between them is
The difference between them is  .The
.The  -intercepts of a line is where the line's
-intercepts of a line is where the line's  -coordinate is
-coordinate is  . The slope is defined as
. The slope is defined as  . Therefore, the line with slope
. Therefore, the line with slope  can be expressed as
can be expressed as![[frac{text{change in }y{-coordinate}}{text{change in }xtext{-coordinate}}=3]](https://latex.artofproblemsolving.com/0/d/a/0da746244106d1f11149908ef3e197c4f8d0cfa4.png) From
From  to the
to the  -intercept, the line must move
-intercept, the line must move  units to the
units to the  -axis. Therefore,
-axis. Therefore,![[frac{text{change in }y{-coordinate}}{text{change in }xtext{-coordinate}}=frac{-15}{x_1}=3implies x_1=-5]](https://latex.artofproblemsolving.com/d/0/0/d005d4b0b7cbb10344b5ec5b531e0f93e7044760.png) .Therefore, the
.Therefore, the  -intercept of the line with slope
-intercept of the line with slope  is
is  .Note that some sources may state "the
.Note that some sources may state "the  -intercept is
-intercept is  " instead of "the
" instead of "the  -intercept is
-intercept is  .
.
If an idea functions great for one part of the problem but does not find the solution to the problem, we want to use the idea again. Using the idea for the line with slope
 , we find
, we find![[frac{text{change in }y{-coordinate}}{text{change in }xtext{-coordinate}}=frac{-15}{x_2}=5implies x_2=-3]](https://latex.artofproblemsolving.com/b/2/a/b2ae5603f3d4d05eb4f618a7f7c57e6bccf57f15.png) . Therefore, the
. Therefore, the  -intercept of the line with slope
-intercept of the line with slope  is
is  . The distance between
. The distance between  .
. - For this problem, we will have to write a three-variable equation, but not necessarily solve it. Let
 and
and  represent the original portions of Al, Betty, and Clare, respectively. At the end of one year, they each have
represent the original portions of Al, Betty, and Clare, respectively. At the end of one year, they each have  and
and  . From this, we can write two equations, marked by (1) and (2).
. From this, we can write two equations, marked by (1) and (2).![[a+b+c=1000]](https://latex.artofproblemsolving.com/7/5/8/758a113c4680a0bbc3ce28fefd61a2e47a8db399.png)
![[(1). text{ }2a+2b+2c=2000]](https://latex.artofproblemsolving.com/4/7/b/47b435cba1e52e1776a9001017791304b42638e4.png)
![[a-100+2b+2c=1500]](https://latex.artofproblemsolving.com/a/e/8/ae8ff2820c248dd9515df1709037eccc86be5e26.png)
![[(2). text{ }a+2b+2c=1600]](https://latex.artofproblemsolving.com/1/2/6/126041f6e69ade4b098b1a4a752abd8081da1690.png) (Equations (1) and (2) are derived from each equation above them.)Since all we need to find is
(Equations (1) and (2) are derived from each equation above them.)Since all we need to find is  subtract the second equation from the first equation to get
subtract the second equation from the first equation to get  Al's original portion was
Al's original portion was  .
. - Let
 and
and  be the digits of
be the digits of  ,
,![[clubsuit(clubsuit(x)) = a + b = 3]](https://latex.artofproblemsolving.com/f/f/4/ff44b47ffecb595f4a6536063ead47ab9c218244.png) Clearly
Clearly  can only be
can only be  or
or  and only
and only  and
and  are possible to have two digits sum to.If
are possible to have two digits sum to.If  sums to
sums to  , there are 3 different solutions :
, there are 3 different solutions :  If
If  sums to
sums to  , there are 7 different solutions:
, there are 7 different solutions:  The total number of solutions is
The total number of solutions is 
![[3^8cdot5^2 = (3^4)^2cdot5^2 = (3^4cdot5)^2 = 405^2]](https://latex.artofproblemsolving.com/f/6/1/f61c9134d3e931ccdcf64326ab0ba2cd581c8b8a.png)
 is not a perfect power, so the smallest possible value of
is not a perfect power, so the smallest possible value of  is
is  .
.- Notice that
 players need to be eliminated for there to be declared a winner. Notice also that every match eliminates exactly one person. Therefore,
players need to be eliminated for there to be declared a winner. Notice also that every match eliminates exactly one person. Therefore,  matches are needed to eliminate
matches are needed to eliminate  people and therefore declare a winner. The rest of the information is irrelevant. Therefore, the total number of matches is
people and therefore declare a winner. The rest of the information is irrelevant. Therefore, the total number of matches is  .28 people receive byes, so in the first round there are
.28 people receive byes, so in the first round there are  matches played. In the second round there are
matches played. In the second round there are  people, so there are 32 matches. In the subsequent rounds, there are
people, so there are 32 matches. In the subsequent rounds, there are  matches played, for a total of
matches played, for a total of  matches. Divisible by 11
matches. Divisible by 11 
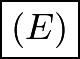 .
. - Let
 be the number of main courses the restaurant serves, so
be the number of main courses the restaurant serves, so  is the number of appetizers. Then the number of dinner combinations is
is the number of appetizers. Then the number of dinner combinations is  . Since the customer wants to eat a different dinner in all
. Since the customer wants to eat a different dinner in all  days of
days of  , we must have
, we must have The smallest integer value that satisfies this is
The smallest integer value that satisfies this is  .Let
.Let  denote the number of main courses needed to meet the requirement. Then the number of dinners available is
denote the number of main courses needed to meet the requirement. Then the number of dinners available is  . Thus
. Thus  must be at least
must be at least  . Since
. Since  ,
,  main courses is enough, but 7 is not. The smallest integer value that satisfies this is
main courses is enough, but 7 is not. The smallest integer value that satisfies this is  .
. - Let
 be the radius of both the cone and the sphere of ice cream, and let
be the radius of both the cone and the sphere of ice cream, and let  be the height of the cone. The cone can hold a maximum of
be the height of the cone. The cone can hold a maximum of  melted ice cream. The volume of the frozen ice cream is
melted ice cream. The volume of the frozen ice cream is  The volume of the melted ice cream is
The volume of the melted ice cream is  of that, which is
of that, which is  Since the melted ice cream fills the cone exactly,
Since the melted ice cream fills the cone exactly, Then the ratio of the cone's height to its radius is
Then the ratio of the cone's height to its radius is 
- For all consecutive odd integers, one of every five is a multiple of 5 and one of every three is a multiple of 3. The answer is
 , so
, so  is the correct answer.
is the correct answer. ![[asy] import graph; unitsize(14mm); defaultpen(linewidth(.8pt)+fontsize(8pt)); dashed=linetype("4 4"); dotfactor=3; pair A=(-2,0), B=(2,0); fill(Arc((0,0),2,0,180)--cycle,mediumgray); fill(Arc((-1,0),1,0,180)--cycle,white); fill(Arc((0,0),1,0,180)--cycle,white); fill(Arc((1,0),1,0,180)--cycle,white); draw(Arc((-1,0),1,60,180)); draw(Arc((0,0),1,0,60),dashed); draw(Arc((0,0),1,60,120)); draw(Arc((0,0),1,120,180),dashed); draw(Arc((1,0),1,0,120)); draw(Arc((0,0),2,0,180)--cycle); dot((0,0)); dot((-1,0)); dot((1,0)); draw((-2,-0.1)--(-2,-0.3),gray); draw((-1,-0.1)--(-1,-0.3),gray); draw((1,-0.1)--(1,-0.3),gray); draw((2,-0.1)--(2,-0.3),gray); label("$A$",A,W); label("$B$",B,E); label("1",(-1.5,-0.1),S); label("2",(0,-0.1),S); label("1",(1.5,-0.1),S); draw((1,0)--(0.5,0.866)); draw((0,0)--(0.5,0.866)); draw((-1,0)--(-0.5,0.866)); draw((0,0)--(-0.5,0.866));[/asy]](https://latex.artofproblemsolving.com/6/f/3/6f30c4091f2ff7d5233d20f8213489e5903af3b6.png) By drawing four lines from the intersect of the semicircles to their centers, we have split the white region into
By drawing four lines from the intersect of the semicircles to their centers, we have split the white region into  of a circle with radius
of a circle with radius  and two equilateral triangles with side length
and two equilateral triangles with side length  . This gives the area of the white region as
. This gives the area of the white region as  . The area of the shaded region is the area of the white region subtracted from the area of the large semicircle. This is equivalent to
. The area of the shaded region is the area of the white region subtracted from the area of the large semicircle. This is equivalent to  .Thus the answer is
.Thus the answer is  .
. because
because  The ratio of
The ratio of  to
to  is
is  since
since  and
and  from subtraction. If we let
from subtraction. If we let  be the height of
be the height of 
![[frac{2}{5} = frac{h-3}{h}]](https://latex.artofproblemsolving.com/1/4/0/140780e0cdc7959d758ae0976f1715fcc6ffbfa0.png)
![[2h = 5h-15]](https://latex.artofproblemsolving.com/d/1/8/d18ea1812352a00725cd0a4938c2adbc85eb9332.png)
![[3h = 15]](https://latex.artofproblemsolving.com/a/0/9/a094622098ec270ad387c750fdeb057742bb8196.png)
![[h = 5]](https://latex.artofproblemsolving.com/a/d/f/adf85c076b2be16b9a1042f4742a0572d100110d.png) The height is
The height is  so the area of
so the area of  is
is  .We can look at this diagram as if it were a coordinate plane with point
.We can look at this diagram as if it were a coordinate plane with point  being
being  . This means that the equation of the line
. This means that the equation of the line  is
is  and the equation of the line
and the equation of the line  is
is  . From this we can set of the follow equation to find the
. From this we can set of the follow equation to find the  coordinate of point
coordinate of point  :
:![[3x=frac{-3}{2}x+frac{15}{2}]](https://latex.artofproblemsolving.com/4/a/c/4ac3116a22f1f37425cc2781f4d32a183bbb294b.png)
![[6x=-3x+15]](https://latex.artofproblemsolving.com/d/c/a/dca5153dba12a953a9ce8c260b780f2ee3374b56.png)
![[9x=15]](https://latex.artofproblemsolving.com/c/9/9/c9904b9484433a55aead3c805324fdec0f7aed94.png)
![[x=frac{5}{3}]](https://latex.artofproblemsolving.com/5/f/b/5fb92a0b1dfdfd971d296b733854fd122d30dcc3.png) We can plug this into one of our original equations to find that the
We can plug this into one of our original equations to find that the  coordinate is
coordinate is  , meaning the area of
, meaning the area of  is
is  At points
At points  and
and  , segment
, segment  is 5 units from segment
is 5 units from segment  . At points
. At points  and
and  , the segments are 2 units from each other. This means that collectively, the two lines closed the distance between them by 3 units over a height of 3 units. Therefore, to close the next two units of distance, they will have to travel a height of 2 units.Then calculate the area of trapezoid
, the segments are 2 units from each other. This means that collectively, the two lines closed the distance between them by 3 units over a height of 3 units. Therefore, to close the next two units of distance, they will have to travel a height of 2 units.Then calculate the area of trapezoid  and triangle
and triangle  separately and add them. The area of the trapezoid is
separately and add them. The area of the trapezoid is  and the area of the triangle is
and the area of the triangle is  .
. 
- We can divide the case of all beads in the bag being red after three replacements into three cases.The first case is in which the two green beads are the first two beads to be chosen. The probability for this is
![[frac{2}{4} times frac{1}{4} times frac{4}{4} = frac{1}{8}]](https://latex.artofproblemsolving.com/c/7/9/c79094610c98c663ffb3d62502cdcc8d8e4bea3a.png) The second case is in which the green beads are chosen first and third. The probability for this is
The second case is in which the green beads are chosen first and third. The probability for this is![[frac{2}{4} times frac{3}{4} times frac{1}{4} = frac{3}{32}]](https://latex.artofproblemsolving.com/7/3/c/73ceeaa46918d0f91fc747ff8f6a3fbc52989dad.png) The third case is in which the green beads are chosen second and third. The probability for this is
The third case is in which the green beads are chosen second and third. The probability for this is![[frac{2}{4} times frac{2}{4} times frac{1}{4} = frac{1}{16}]](https://latex.artofproblemsolving.com/8/9/2/892342fa379797a31251d5885c6957b04e601ee8.png) Add all these cases together
Add all these cases together![[frac{1}{8}+frac{3}{32}+frac{1}{16} = frac{4}{32}+frac{3}{32}+frac{2}{32} = boxed{textbf{(C) } frac{9}{32}}]](https://latex.artofproblemsolving.com/b/5/8/b582cc507ddc9c4ad70f25708252281aeab43997.png)
- First, find how many chimes will have already happened before midnight (the beginning of the day) of

 half-hours have passed, and the number of chimes according to the hour is
half-hours have passed, and the number of chimes according to the hour is  The total number of chimes is
The total number of chimes is  Every day, there will be
Every day, there will be  half-hours and
half-hours and  chimes according to the arrow, resulting in
chimes according to the arrow, resulting in  total chimes.On
total chimes.On  the number of chimes that still need to occur is
the number of chimes that still need to occur is 
 Rounding up, it is
Rounding up, it is  days past
days past  which is
which is 
- Here is an easy way to look at this, where
 is the perimeter, and
is the perimeter, and  is the apothem:Area of Octagon:
is the apothem:Area of Octagon:  .Area of Rectangle:
.Area of Rectangle:  .You can see from this that the octagon's area is twice as large as the rectangle's area is
.You can see from this that the octagon's area is twice as large as the rectangle's area is  .
.![[asy] unitsize(1cm); defaultpen(linewidth(.8pt)+fontsize(8pt)); pair C=dir(22.5), B=dir(67.5), A=dir(112.5), H=dir(157.5), G=dir(202.5), F=dir(247.5), E=dir(292.5), D=dir(337.5); draw(A--B--C--D--E--F--G--H--cycle); label("$A$",A,NNW); label("$B$",B,NNE); label("$C$",C,ENE); label("$D$",D,ESE); label("$E$",E,SSE); label("$F$",F,SSW); label("$G$",G,WSW); label("$H$",H,WNW); draw(A--E--F--B--C--G--H--D); draw(A--E--F--B--A,blue); draw(A--F--E--B--A,red); [/asy]](https://latex.artofproblemsolving.com/a/8/a/a8a9e9c63ae7f93d28c6a8e83ab8b76c83a6f147.png) Here is a less complicated way than that of the user above. If you draw a line segment from each vertex to the center of the octagon and draw the rectangle ABEF( In red), you can see that two of the triangles (In blue) share the same base and height with half the rectangle. Therefore, the rectangle's area is the same as 4 of the 8 triangles, and is
Here is a less complicated way than that of the user above. If you draw a line segment from each vertex to the center of the octagon and draw the rectangle ABEF( In red), you can see that two of the triangles (In blue) share the same base and height with half the rectangle. Therefore, the rectangle's area is the same as 4 of the 8 triangles, and is  the area of the octagon.
the area of the octagon.![[asy] unitsize(1cm); defaultpen(linewidth(.8pt)+fontsize(8pt)); pair C=dir(22.5), B=dir(67.5), A=dir(112.5), H=dir(157.5), G=dir(202.5), F=dir(247.5), E=dir(292.5), D=dir(337.5); draw(A--B--C--D--E--F--G--H--cycle); label("$A$",A,NNW); label("$B$",B,NNE); label("$C$",C,ENE); label("$D$",D,ESE); label("$E$",E,SSE); label("$F$",F,SSW); label("$G$",G,WSW); label("$H$",H,WNW); draw(A--D--E--H--G--B--C--F); [/asy]](https://latex.artofproblemsolving.com/a/8/3/a83fa1ab65b5ad398b3743d61186fe7a87c34209.png) Drawing lines
Drawing lines  ,
,  ,
,  , and
, and  , we can see that the octagon is comprised of
, we can see that the octagon is comprised of  square,
square,  rectangles, and
rectangles, and  triangles. The triangles each are
triangles. The triangles each are  triangles, and since their diagonal is length
triangles, and since their diagonal is length  , each of their sides is
, each of their sides is  . The area of the entire figure is, likewise,
. The area of the entire figure is, likewise,  (the square)
(the square) (the 4 rectangles)
(the 4 rectangles) (the triangles), which simplifies to
(the triangles), which simplifies to  . The area of
. The area of  is just
is just  , or
, or  +
+  , which we can see is the area of
, which we can see is the area of  the area of the octagon.
the area of the octagon. - The difference between consecutive terms is
 Therefore we can also express the third and fourth terms as
Therefore we can also express the third and fourth terms as  and
and  Then we can set them equal to
Then we can set them equal to  and
and  because they are the same thing.
because they are the same thing. Substitute into our other equation.
Substitute into our other equation.![[frac{x}{y}=x-5y]](https://latex.artofproblemsolving.com/7/4/4/7447ff4042273b628b683c0be7a6adb782094cc4.png)
![[frac{-3}{y-1}=frac{-3y}{y-1}-5y]](https://latex.artofproblemsolving.com/e/a/f/eafd224e1b0406671c0ea78a89f70250ab4d9598.png)
![[-3=-3y-5y(y-1)]](https://latex.artofproblemsolving.com/5/8/2/582e642d7ac3fe394341c104bb678404cf1937d6.png)
![[0=5y^2-2y-3]](https://latex.artofproblemsolving.com/4/f/c/4fc65b027cacf27699496e8f7a46167eb301ea72.png)
![[0=(5y+3)(y-1)]](https://latex.artofproblemsolving.com/2/7/1/2715b828ebf0e900ba0d1a4a4409393b2d5c9683.png)
![[y=-frac35, 1]](https://latex.artofproblemsolving.com/2/b/f/2bf85034e5c754150e8e99435ec811627279e560.png) But
But  cannot be
cannot be  because then every term would be equal to
because then every term would be equal to  Therefore
Therefore  Substituting the value for
Substituting the value for  into any of the equations, we get
into any of the equations, we get  Finally,
Finally,![[frac{x}{y}-2y=frac{9cdot 5}{8cdot 3}+frac{6}{5}=boxed{textbf{(E)} frac{123}{40}}]](https://latex.artofproblemsolving.com/5/5/e/55e30872e72c0aa052d66c068d2af833a675a508.png)
- To test if a number is divisible by three, you add up the digits of the number. If the sum is divisible by three, then the original number is a multiple of three. If the sum is too large, you can repeat the process until you can tell whether it is a multiple of three. This is the basis for the solution. Since the last two digits are
 , the sum of the digits is
, the sum of the digits is  (therefore it is not divisible by three). However certain numbers can be added to make the sum of the digits a multiple of three.
(therefore it is not divisible by three). However certain numbers can be added to make the sum of the digits a multiple of three. ,
, , and so on.However since the largest four-digit number ending with
, and so on.However since the largest four-digit number ending with  is
is  , the maximum sum is
, the maximum sum is .Using that process we can fairly quickly compile a list of the sum of the first two digits of the number.
.Using that process we can fairly quickly compile a list of the sum of the first two digits of the number.![[{1, 4, 7, 10, 13, 16}]](https://latex.artofproblemsolving.com/6/4/d/64ddcf298f712b3a213eeb5a83e875865ccb8407.png) Now we find all the two-digit numbers that have any of the sums shown above. We can do this by listing all the two digit numbers
Now we find all the two-digit numbers that have any of the sums shown above. We can do this by listing all the two digit numbers  in separate cases.
in separate cases.
![[I. x+y = 1, {10} = 1]](https://latex.artofproblemsolving.com/9/4/3/943a6fca640b2ef0375212e22d8e53b886155d61.png)
![[II. x+y = 4, {13, 22, 31, 40} = 4]](https://latex.artofproblemsolving.com/e/9/e/e9e1cddd5cb18b50d8e6a3fbf53287d9ebe3f467.png)
![[III. x+y = 7, {16, 25, 34, 43, 52, 61, 70} = 7]](https://latex.artofproblemsolving.com/c/5/3/c53383c2670ef646e03ed75d328e01a70c39bba7.png)
![[IV. x+y = 10, {19, 28, 37, 46, 55, 64, 73, 82, 91} = 9]](https://latex.artofproblemsolving.com/8/c/9/8c9642d529a637ed6678565dacbf2b8dd86221a9.png)
![[V. x+y = 13, {49, 58, 67, 76, 85, 94} = 6]](https://latex.artofproblemsolving.com/e/5/d/e5db4469f46fe2074b96fed15d09fef52f30de45.png)
![[VI. x+y = 16, {79, 88, 97} = 3]](https://latex.artofproblemsolving.com/a/f/a/afa411e8f5ae7e3ba4228cd38945cec13c3180c7.png)
And finally, we add the number of elements in each set.
![[1+4+7+9+6+3 = boxed{textbf{(B)} 30}]](https://latex.artofproblemsolving.com/9/1/0/91018c437f8d8e47a97363f6d79fa803645ae6e7.png)
A number divisible by
 has all its digits add to a multiple of
has all its digits add to a multiple of  The last two digits are
The last two digits are  and
and  and add up to
and add up to  Therefore the first two digits must add up to
Therefore the first two digits must add up to 
 digits (including
digits (including  ) are
) are 
 are
are  and
and  are
are  The following combinations are equivalent to
The following combinations are equivalent to  :
:![[0 (text{mod} 3)+1 (text{mod} 3) equiv 1 (text{mod} 3)+0 (text{mod} 3) equiv 2 (text{mod} 3) +2 (text{mod} 3)]](https://latex.artofproblemsolving.com/2/c/d/2cde0c1540ededeb77780da629a47fff63361977.png)
Let the first term in each combination represent the thousands digit and the second term represent the hundreds digit. We can use this to find the total amount of four-digit numbers.
![[3cdot3 + 3cdot4 + 3cdot3 = 9 + 12 + 9 = boxed{textbf{(B)} 30}]](https://latex.artofproblemsolving.com/0/a/5/0a57342d9ed7b8da88c30c113012d36f02e40212.png)
We have the following:
 and
and  . Then
. Then  for some integers
for some integers  and
and  . Taking mod 3 gives:
. Taking mod 3 gives:  so
so  for some integer
for some integer  . But
. But  so
so  . Bounding this gives us:
. Bounding this gives us:  so
so  . Dividing by
. Dividing by  gives
gives  so
so  . This gives
. This gives 
The number is in the form

Notice that the number is divisible by
 if the sum of the digits of
if the sum of the digits of  is divisible by
is divisible by 
Our first number that is divisible by
 is
is  , next is
, next is  .. Notice
.. Notice  goes from
goes from 
Hence, there are
 distinct four digit numbers.
distinct four digit numbers.Following the form
 in Solution 4, notice that
in Solution 4, notice that  to satisfy our condition. Choose a value of
to satisfy our condition. Choose a value of  from 1 to 9. For
from 1 to 9. For  , there are exactly 4 values of
, there are exactly 4 values of  . For the remaining 6 digits, there are 3 choices for y. So our answer is
. For the remaining 6 digits, there are 3 choices for y. So our answer is  .
.There are
 possible values for the first two digits. One-third of them yield a multiple of
possible values for the first two digits. One-third of them yield a multiple of  , so the answer is
, so the answer is 
以上解析方式仅供参考
学术活动报名扫码了解!免费领取历年真题!
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





