- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
2009 USAMO Problems真题及答案
2009 USAMO Problems真题及答案
完整版真题免费下载
+答案解析请参考文末
真题下载请前往【纯真题】小程序
Day 1
Problem 1
Given circles ![]() and
and ![]() intersecting at points
intersecting at points ![]() and
and ![]() , let
, let ![]() be a line through the center of
be a line through the center of ![]() intersecting
intersecting ![]() at points
at points ![]() and
and ![]() and let
and let ![]() be a line through the center of
be a line through the center of ![]() intersecting
intersecting ![]() at points
at points ![]() and
and ![]() . Prove that if
. Prove that if ![]() and
and ![]() lie on a circle then the center of this circle lies on line
lie on a circle then the center of this circle lies on line ![]() .
.
Problem 2
Let ![]() be a positive integer. Determine the size of the largest subset of
be a positive integer. Determine the size of the largest subset of ![]() which does not contain three elements
which does not contain three elements ![]() (not necessarily distinct) satisfying
(not necessarily distinct) satisfying ![]() .
.
Problem 3
We define a chessboard polygon to be a polygon whose sides are situated along lines of the form ![]() or
or ![]() , where
, where ![]() and
and ![]() are integers. These lines divide the interior into unit squares, which are shaded alternately grey and white so that adjacent squares have different colors. To tile a chessboard polygon by dominoes is to exactly cover the polygon by non-overlapping
are integers. These lines divide the interior into unit squares, which are shaded alternately grey and white so that adjacent squares have different colors. To tile a chessboard polygon by dominoes is to exactly cover the polygon by non-overlapping ![]() rectangles. Finally, a tasteful tiling is one which avoids the two configurations of dominoes shown on the left below. Two tilings of a
rectangles. Finally, a tasteful tiling is one which avoids the two configurations of dominoes shown on the left below. Two tilings of a ![]() rectangle are shown; the first one is tasteful, while the second is not, due to the vertical dominoes in the upper right corner.
rectangle are shown; the first one is tasteful, while the second is not, due to the vertical dominoes in the upper right corner.
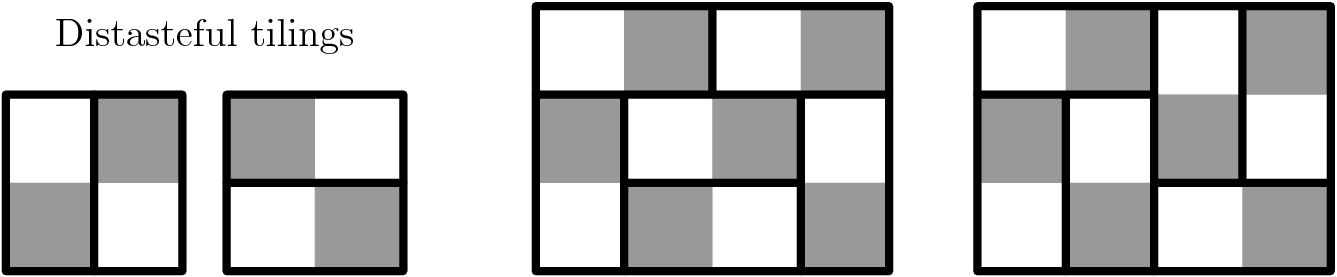
a) Prove that if a chessboard polygon can be tiled by dominoes, then it can be done so tastefully.
b) Prove that such a tasteful tiling is unique.
Day 2
Problem 4
For ![]() let
let ![]() ,
, ![]() , ...,
, ..., ![]() be positive real numbers such that
be positive real numbers such that
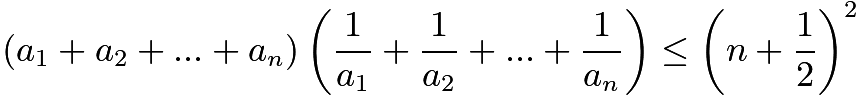 Prove that
Prove that ![]() .
.
Problem 5
Trapezoid ![]() , with
, with ![]() , is inscribed in circle
, is inscribed in circle ![]() and point
and point ![]() lies inside triangle
lies inside triangle ![]() . Rays
. Rays ![]() and
and ![]() meet
meet ![]() again at points
again at points ![]() and
and ![]() , respectively. Let the line through
, respectively. Let the line through ![]() parallel to
parallel to ![]() intersect
intersect ![]() and
and ![]() at points
at points ![]() and
and ![]() , respectively. Prove that quadrilateral
, respectively. Prove that quadrilateral ![]() is cyclic if and only if
is cyclic if and only if ![]() bisects
bisects ![]() .
.
Problem 6
Let ![]() be an infinite, nonconstant sequence of rational numbers, meaning it is not the case that
be an infinite, nonconstant sequence of rational numbers, meaning it is not the case that ![]() Suppose that
Suppose that ![]() is also an infinite, nonconstant sequence of rational numbers with the property that
is also an infinite, nonconstant sequence of rational numbers with the property that ![]() is an integer for all
is an integer for all ![]() and
and ![]() . Prove that there exists a rational number
. Prove that there exists a rational number ![]() such that
such that ![]() and
and ![]() are integers for all
are integers for all ![]() and
and ![]() .
.
[wechat keyword="usamo" key="usamohanlin"]
Problem 1
Solution
Let ![]() be the circumcircle of
be the circumcircle of ![]() ,
, ![]() to be the radius of
to be the radius of ![]() , and
, and ![]() to be the center of the circle
to be the center of the circle ![]() , where
, where ![]() . Note that
. Note that ![]() and
and ![]() are the radical axises of
are the radical axises of ![]() ,
, ![]() and
and ![]() ,
, ![]() respectively. Hence, by power of a point(the power of
respectively. Hence, by power of a point(the power of ![]() can be expressed using circle
can be expressed using circle ![]() and
and ![]() and the power of
and the power of ![]() can be expressed using circle
can be expressed using circle ![]() and
and ![]() ),
),![]()
![]() Subtracting these two equations yields that
Subtracting these two equations yields that ![]() , so
, so ![]() must lie on the radical axis of
must lie on the radical axis of ![]() ,
, ![]() .
.
~AopsUser101
Remarks
Conveniently, this analytic solution takes care of all configuration issues we may have encountered had we used a more traditional solution, such as angle-chasing(which would indeed work, just be considerably less elegant).
~AopsUser101
Problem 2
Solution 1
Let ![]() be a subset of
be a subset of ![]() of largest size satisfying
of largest size satisfying ![]() for all
for all ![]() . First, observe that
. First, observe that ![]() . Next note that
. Next note that ![]() , by observing that the set of all the odd numbers in
, by observing that the set of all the odd numbers in ![]() works. To prove that
works. To prove that ![]() , it suffices to only consider even
, it suffices to only consider even ![]() , because the statement for
, because the statement for ![]() implies the statement for
implies the statement for ![]() as well. So from here forth, assume
as well. So from here forth, assume ![]() is even.
is even.
For any two sets ![]() and
and ![]() , denote by
, denote by ![]() the set
the set ![]() , and by
, and by ![]() the set
the set ![]() . Also, let
. Also, let ![]() denote
denote ![]() and
and ![]() denote
denote ![]() . First, we present a lemma:
. First, we present a lemma:
Lemma 1: Let ![]() and
and ![]() be two sets of integers. Then
be two sets of integers. Then ![]() .
.
Proof: Write ![]() and
and ![]() where
where ![]() and
and ![]() . Then
. Then ![]() is a strictly increasing sequence of
is a strictly increasing sequence of ![]() integers in
integers in ![]() .
.
Now, we consider two cases:
Case 1: One of ![]() is not in
is not in ![]() . Without loss of generality, suppose
. Without loss of generality, suppose ![]() . Let
. Let ![]() (a set with
(a set with ![]() elements), so that
elements), so that ![]() by our assumption. Now, the condition that
by our assumption. Now, the condition that ![]() for all
for all ![]() implies that
implies that ![]() . Since any element of
. Since any element of ![]() has absolute value at most
has absolute value at most ![]() , we have
, we have ![]() . It follows that
. It follows that ![]() , so
, so ![]() . However, by Lemma 1, we also have
. However, by Lemma 1, we also have ![]() . Therefore, we must have
. Therefore, we must have ![]() , or
, or ![]() , or
, or ![]() .
.
Case 2: Both ![]() and
and ![]() are in
are in ![]() . Then
. Then ![]() and
and ![]() are not in
are not in ![]() , and at most one of each of the pairs
, and at most one of each of the pairs 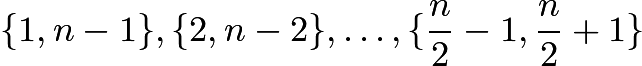 and their negatives are in
and their negatives are in ![]() . This means
. This means ![]() contains at most
contains at most ![]() elements.
elements.
Thus we have proved that ![]() for even
for even ![]() , and we are done.
, and we are done.
Solution 2
Let ![]() be the set of subsets satisfying the
be the set of subsets satisfying the ![]() condition for
condition for ![]() , and let
, and let ![]() be the largest size of a set in
be the largest size of a set in ![]() . Let
. Let ![]() if
if ![]() is even, and
is even, and ![]() if
if ![]() is odd. We note that
is odd. We note that ![]() due to the following constuction:
due to the following constuction:![]() or all of the odd numbers in the set. Then the sum of any three will be odd and thus nonzero.
or all of the odd numbers in the set. Then the sum of any three will be odd and thus nonzero.
Lemma 1: ![]() . If
. If ![]() , then we note that
, then we note that ![]() , so
, so ![]() .
. ![]()
Lemma 2: ![]() . Suppose, for sake of contradiction, that
. Suppose, for sake of contradiction, that ![]() and
and ![]() . Remove
. Remove ![]() from
from ![]() , and partition the rest of the elements into two sets
, and partition the rest of the elements into two sets ![]() , where
, where ![]() and
and ![]() contain all of the positive and negative elements of
contain all of the positive and negative elements of ![]() , respectively. (obviously
, respectively. (obviously ![]() , because
, because ![]() ). WLOG, suppose
). WLOG, suppose ![]() . Then
. Then ![]() . We now show the following two sub-results:
. We now show the following two sub-results:
Sub-lemma (A): if ![]() ,
, ![]() [and similar for
[and similar for ![]() ]; andSub-lemma (B): we cannot have both
]; andSub-lemma (B): we cannot have both ![]() and
and ![]() simultaneously hold.
simultaneously hold.
This is sufficient, because the only two elements that may be in ![]() that are not in
that are not in ![]() are
are ![]() and
and ![]() ; for
; for ![]() , we must either have
, we must either have ![]() and both
and both ![]() [but by pigeonhole
[but by pigeonhole ![]() , see sub-lemma (A)], or
, see sub-lemma (A)], or ![]() , and
, and ![]() , in which case by (A) we must have
, in which case by (A) we must have ![]() , violating (B).
, violating (B).
(A): Partition ![]() into the
into the ![]() sets
sets ![]() . Because
. Because ![]() , then if any of those sets are within
, then if any of those sets are within ![]() ,
, ![]() . But by Pigeonhole at most
. But by Pigeonhole at most ![]() elements may be in
elements may be in ![]() , contradiction.
, contradiction.
(B): We prove this statement with another induction. We see that the statement easily holds true for ![]() or
or ![]() , so suppose it is true for
, so suppose it is true for ![]() , but [for sake of contradiction] false for
, but [for sake of contradiction] false for ![]() . Let
. Let ![]() , and similarly for
, and similarly for ![]() . Again WLOG
. Again WLOG ![]() . Then we have
. Then we have ![]() .
.
If ![]() , then by inductive hypothesis, we must have
, then by inductive hypothesis, we must have ![]() . But (A) implies that we cannot add
. But (A) implies that we cannot add ![]() or
or ![]() . So to satisfy
. So to satisfy ![]() we must have
we must have ![]() added, but then
added, but then ![]() contradiction.
contradiction.
If ![]() , then at least three of
, then at least three of ![]() added. But
added. But ![]() , and by (A) we have that
, and by (A) we have that ![]() cannot be added. If
cannot be added. If ![]() , then another grouping similar to (A) shows that
, then another grouping similar to (A) shows that ![]() canno be added, contradiction. So
canno be added, contradiction. So ![]() ,
, ![]() , and adding the three remaining elements gives
, and adding the three remaining elements gives ![]() contradiction.
contradiction.
If ![]() , then all four of
, then all four of ![]() must be added, and furthermore
must be added, and furthermore ![]() . Then
. Then ![]() , and by previous paragraph we cannot add
, and by previous paragraph we cannot add ![]() .
. ![]()
So we have 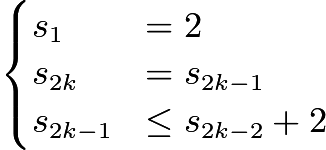 and by induction, that
and by induction, that 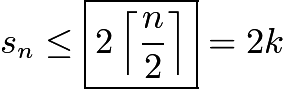 , which we showed is achievable above.
, which we showed is achievable above.
Problem 3
暂无官方Solutions,可联系翰林导师进行详解。欢迎点击联系我们资讯翰林顾问!
Problem 4
Solution
Assume without loss of generality that ![]() . Now we seek to prove that
. Now we seek to prove that ![]() .
.
By the Cauchy-Schwarz Inequality,![]() Since
Since ![]() , clearly
, clearly 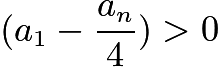 , dividing yields:
, dividing yields:
![]()
as desired.
Problem 5
Solution 1
We will use directed angles in this solution. Extend ![]() to
to ![]() as follows:
as follows:
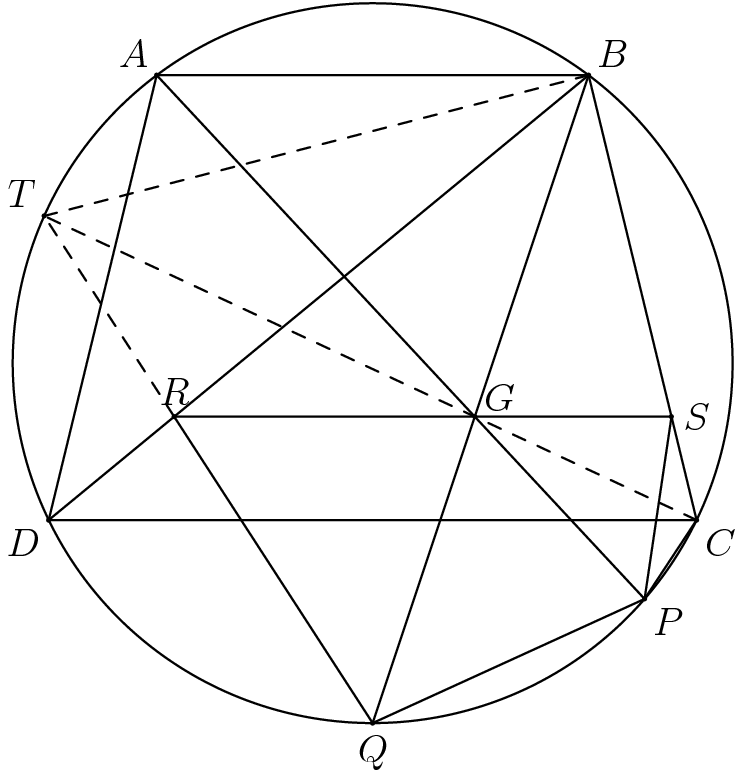 If:
If:
Note that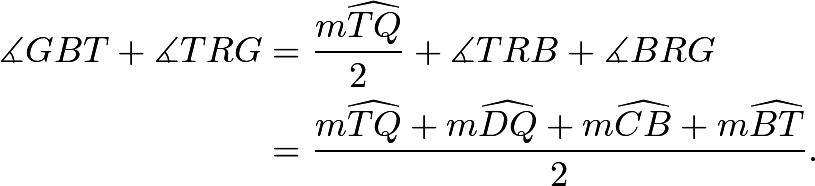 Thus,
Thus, ![]() is cyclic.
is cyclic.
Also, note that ![]() is cyclic because
is cyclic because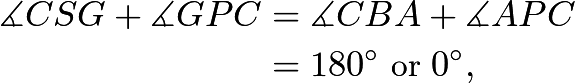 depending on the configuration.
depending on the configuration.
Next, we have ![]() are collinear since
are collinear since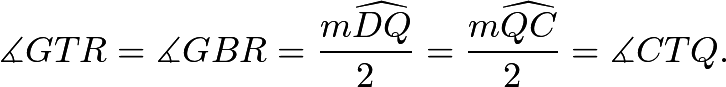
Therefore,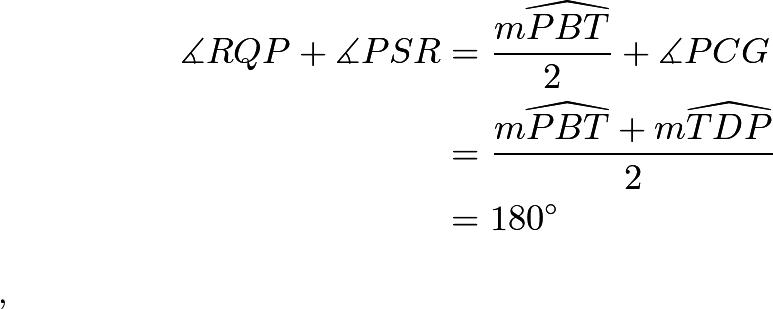 so
so ![]() is cyclic.
is cyclic.
Only If: These steps can be reversed.
Solution 2 (Projective)
Extend ![]() to
to ![]() , and let line
, and let line ![]() intersect
intersect ![]() at
at ![]() and another point
and another point ![]() , as shown:
, as shown:
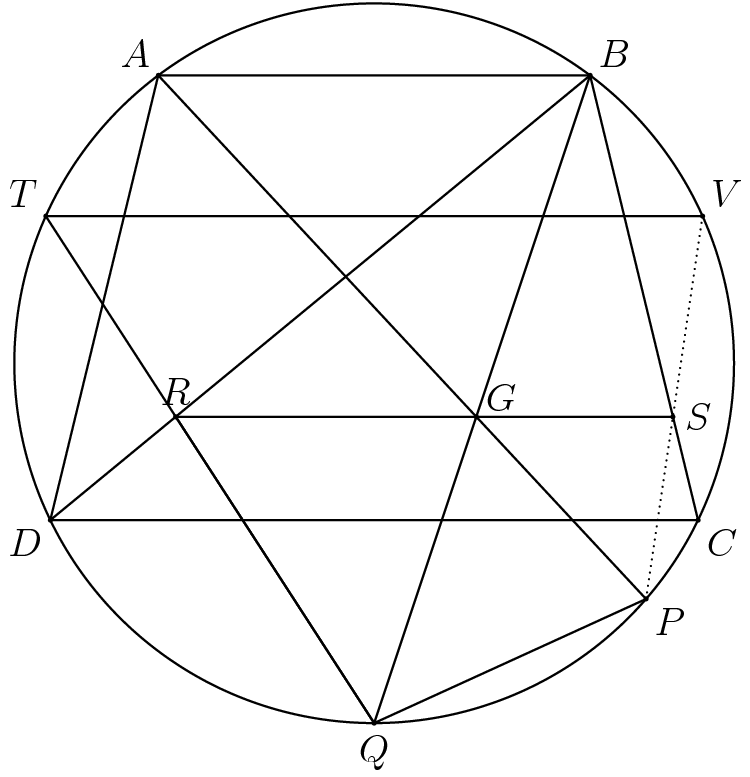
If:
Suppose that ![]() , and
, and ![]() . Pascal's theorem on the tuple
. Pascal's theorem on the tuple ![]() implies that the points
implies that the points ![]() ,
, ![]() , and
, and ![]() are collinear. However,
are collinear. However, ![]() and
and ![]() are symmetrical with respect to the axis of symmetry of trapezoid
are symmetrical with respect to the axis of symmetry of trapezoid ![]() , and
, and ![]() and
and ![]() are also symmetrical with respect to the axis of symmetry of
are also symmetrical with respect to the axis of symmetry of ![]() (as
(as ![]() is the midpoint of
is the midpoint of ![]() , and
, and ![]() ). Since
). Since ![]() ,
, ![]() and
and ![]() are symmetric with respect to the axis of symmetry of trapezoid
are symmetric with respect to the axis of symmetry of trapezoid ![]() . This implies that line
. This implies that line ![]() is equivalent to line
is equivalent to line ![]() . Thus,
. Thus, ![]() lies on line
lies on line ![]() . However,
. However, ![]() , so this implies that
, so this implies that ![]() .
.
Now note that ![]() is cyclic. Since
is cyclic. Since ![]() ,
, ![]() . However,
. However, ![]() . Therefore,
. Therefore, ![]() is cyclic.
is cyclic.
Only If:
Consider the same setup, except ![]() is no longer the midpoint of
is no longer the midpoint of ![]() . Note that
. Note that ![]() must be parallel to
must be parallel to ![]() in order for
in order for ![]() to be cyclic. We claim that
to be cyclic. We claim that ![]() and hope to reach a contradiction. Pascal's theorem on the tuple
and hope to reach a contradiction. Pascal's theorem on the tuple ![]() implies that
implies that ![]() ,
, ![]() , and
, and ![]() are collinear. However, there exists a unique point
are collinear. However, there exists a unique point ![]() such that
such that ![]() ,
, ![]() , and
, and ![]() are concurrent. By If,
are concurrent. By If, ![]() must be the midpoint of
must be the midpoint of ![]() in order for the concurrency to occur; hence,
in order for the concurrency to occur; hence, ![]() . Then
. Then ![]() , since
, since ![]() . However, this is a contradiction, so therefore
. However, this is a contradiction, so therefore ![]() cannot be parallel to
cannot be parallel to ![]() and
and ![]() is not cyclic.
is not cyclic.
Solution by TheBoomBox77
Problem 6
暂无官方Solutions,可联系翰林导师进行详解。欢迎点击联系我们资讯翰林顾问!
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





