- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
USACO 2016 February Contest, Bronze Problem 3. Load Balancing
原题下载
答案
(Analysis by Nick Wu)
There are a lot of possible fence combinations to consider - if we simply consider every possible even x-coordinate and every possible event y-coordinate, there would be 50000025000002 different combinations which is far too many.
Let us take an extreme example where there are two cows, one at (1,1)(1,1) and the other at (999999,999999)(999999,999999). Note that every even x-coordinate between 22 and 999998999998 yields exactly the same division of cows into quadrants, no matter which y-coordinate we pick. By the same logic, every even y-coordinate between 22 and 999998999998 yields exactly the same division of cows into quadrants.
Therefore, we can make the following observation - if we set the vertical fence at x=ax=a but no cow is placed with an x-coordinate of a−1a−1, we can move the vertical fence to x=a−2x=a−2 and still preserve the same division of cows into quadrants. Similarly, if we set the horizontal fence at y=by=b but no cow is placed with a y-coordinate at y=b−1y=b−1, we can move the horizontal fence to y=b−2y=b−2.
This means that we only need to place vertical fences where x=ax=a and there is a cow with x-coordinate a−1a−1, and we only need to place vertical fences where y=by=b and there is a cow with y-coordinate b−1b−1.
This gives us at most ten thousand pairs to try, which is small enough.
Here is my Java code:
import java.io.*;
import java.util.*;
public class balancing {
public static void main(String[] args) throws IOException {
// initialize file I/O
BufferedReader br = new BufferedReader(new FileReader("balancing.in"));
PrintWriter pw = new PrintWriter(new BufferedWriter(new FileWriter("balancing.out")));
// read in N, we can safely ignore B so we don't actually read the value
StringTokenizer st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken());
// create arrays to store locations of cows
// cow i is at point (xLoc[i], yLoc[i])
int[] xLoc = new int[n];
int[] yLoc = new int[n];
for(int i = 0; i < n; i++) {
// read in location of cow i
st = new StringTokenizer(br.readLine());
xLoc[i] = Integer.parseInt(st.nextToken());
yLoc[i] = Integer.parseInt(st.nextToken());
}
// in the absolute worst case, N cows will be in one quadrant
int ans = n;
for(int xIndex = 0; xIndex < n; xIndex++) {
for(int yIndex = 0; yIndex < n; yIndex++) {
// identify the fence location
// vertical fence at x=xDiv
// horizontal fence at y=yDiv
int xDiv = xLoc[xIndex]+1;
int yDiv = yLoc[yIndex]+1;
int upperLeft = 0;
int upperRight = 0;
int lowerLeft = 0;
int lowerRight = 0;
// identify which quadrant each cows lands in
for(int i = 0; i < n; i++) {
if(xLoc[i] < xDiv && yLoc[i] < yDiv) {
lowerLeft++;
}
if(xLoc[i] < xDiv && yLoc[i] > yDiv) {
upperLeft++;
}
if(xLoc[i] > xDiv && yLoc[i] < yDiv) {
lowerRight++;
}
if(xLoc[i] > xDiv && yLoc[i] > yDiv) {
upperRight++;
}
}
// figure out which region has the most cows
int worstRegion = 0;
if(upperLeft > worstRegion) {
worstRegion = upperLeft;
}
if(upperRight > worstRegion) {
worstRegion = upperRight;
}
if(lowerLeft > worstRegion) {
worstRegion = lowerLeft;
}
if(lowerRight > worstRegion) {
worstRegion = lowerRight;
}
// determine if we have found a better pair of fences
if(worstRegion < ans) {
ans = worstRegion;
}
}
}
// print the answer
pw.println(ans);
// close output stream
pw.close();
}
}
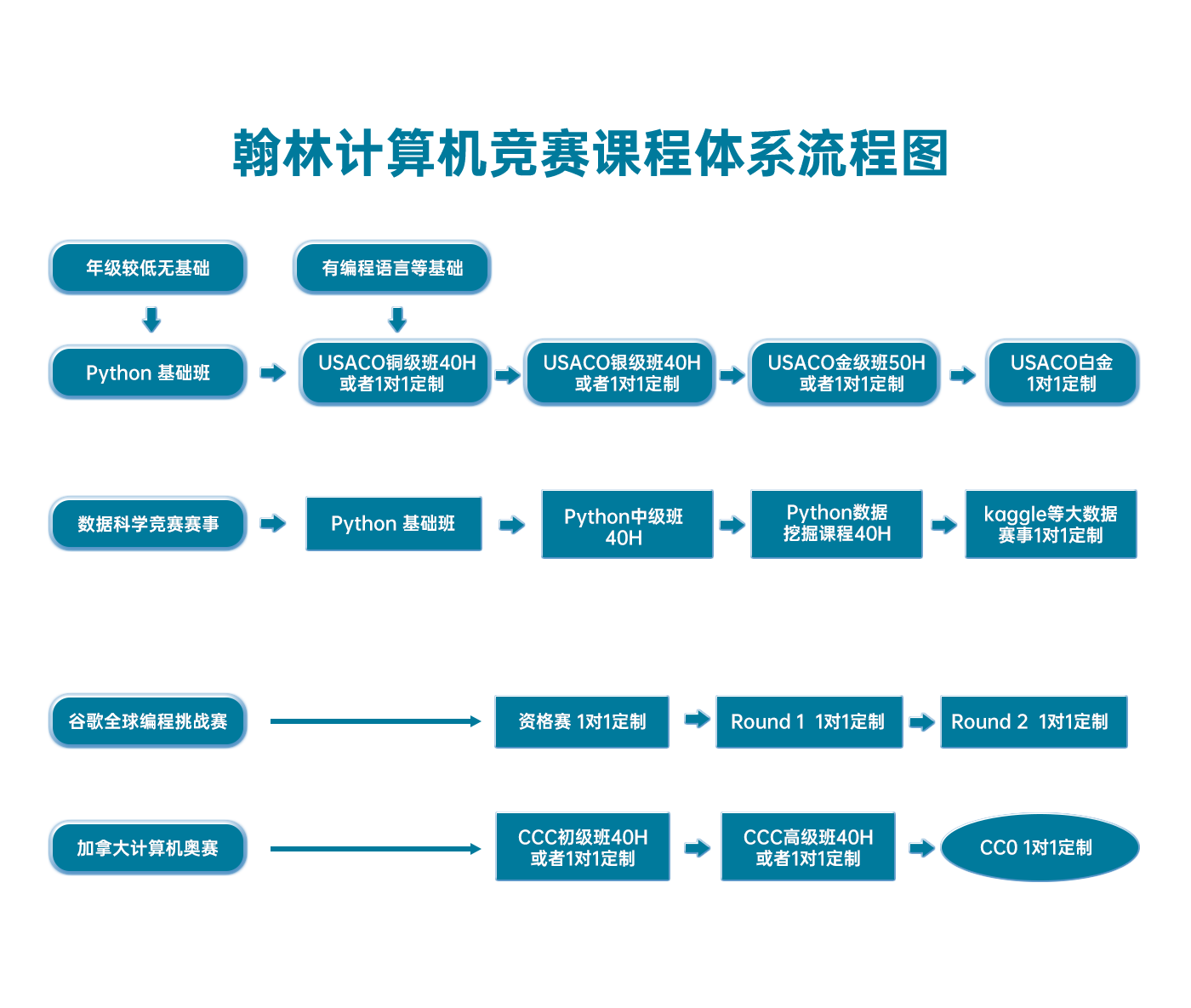
翰林USACO课程体系流程图
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





