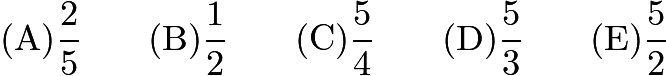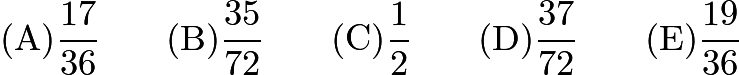- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
2007 AMC 8 真题与答案及免费中文视频详解(翰林独家)
2007 AMC 8 Problems & Solutions
2007 AMC 8 真题与答案及中文视频详解(翰林独家)
Problem 1
Theresa's parents have agreed to buy her tickets to see her favorite band if she spends an average of ![]() hours per week helping around the house for
hours per week helping around the house for ![]() weeks. For the first
weeks. For the first ![]() weeks she helps around the house for
weeks she helps around the house for ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]() hours. How many hours must she work for the final week to earn the tickets?
hours. How many hours must she work for the final week to earn the tickets?
![]()
Problem 2
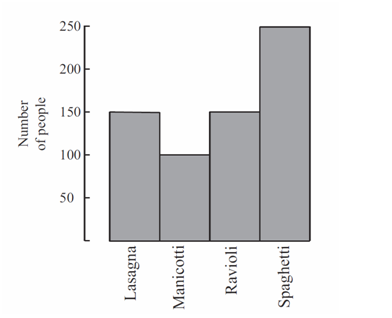
![]() students were surveyed about their pasta preferences. The choices were lasagna, manicotti, ravioli and spaghetti. The results of the survey are displayed in the bar graph. What is the ratio of the number of students who preferred spaghetti to the number of students who preferred manicotti?
students were surveyed about their pasta preferences. The choices were lasagna, manicotti, ravioli and spaghetti. The results of the survey are displayed in the bar graph. What is the ratio of the number of students who preferred spaghetti to the number of students who preferred manicotti?
Problem 3
What is the sum of the two smallest prime factors of ![]() ?
?
![]()
Problem 4
A haunted house has six windows. In how many ways can Georgie the Ghost enter the house by one window and leave by a different window?
![]()
Problem 5
Chandler wants to buy a ![]() mountain bike. For his birthday, his grandparents send him
mountain bike. For his birthday, his grandparents send him ![]() , his aunt sends him
, his aunt sends him ![]() and his cousin gives him
and his cousin gives him ![]() . He earns
. He earns ![]() per week for his paper route. He will use all of his birthday money and all of the money he earns from his paper route. In how many weeks will he be able to buy the mountain bike?
per week for his paper route. He will use all of his birthday money and all of the money he earns from his paper route. In how many weeks will he be able to buy the mountain bike?
![]()
Problem 6
The average cost of a long-distance call in the USA in ![]() was
was ![]() cents per minute, and the average cost of a long-distance call in the USA in
cents per minute, and the average cost of a long-distance call in the USA in ![]() was
was ![]() cents per minute. Find the approximate percent decrease in the cost per minute of a long- distance call.
cents per minute. Find the approximate percent decrease in the cost per minute of a long- distance call.
![]()
Problem 7
The average age of ![]() people in a room is
people in a room is ![]() years. An
years. An ![]() -year-old person leaves the room. What is the average age of the four remaining people?
-year-old person leaves the room. What is the average age of the four remaining people?
![]()
Problem 10
For any positive integer ![]() , define
, define ![]() to be the sum of the positive factors of
to be the sum of the positive factors of ![]() . For example,
. For example, ![]() . Find
. Find  .
.
![]()
Problem 11
(解析视频请点击Problem 12下方视频)
Tiles ![]() and
and ![]() are translated so one tile coincides with each of the rectangles
are translated so one tile coincides with each of the rectangles ![]() and
and ![]() . In the final arrangement, the two numbers on any side common to two adjacent tiles must be the same. Which of the tiles is translated to Rectangle
. In the final arrangement, the two numbers on any side common to two adjacent tiles must be the same. Which of the tiles is translated to Rectangle ![]() ?
?
Problem 12
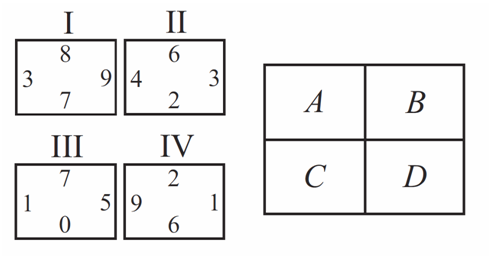
A unit hexagram is composed of a regular hexagon of side length ![]() and its
and its ![]() equilateral triangular extensions, as shown in the diagram. What is the ratio of the area of the extensions to the area of the original hexagon?
equilateral triangular extensions, as shown in the diagram. What is the ratio of the area of the extensions to the area of the original hexagon?
Problem 13
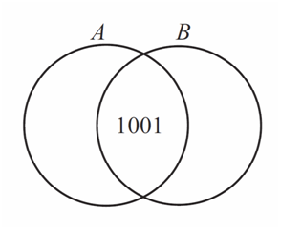
Sets ![]() and
and ![]() , shown in the Venn diagram, have the same number of elements. Their union has
, shown in the Venn diagram, have the same number of elements. Their union has ![]() elements and their intersection has
elements and their intersection has ![]() elements. Find the number of elements in
elements. Find the number of elements in ![]() .
.
Problem 14
The base of isosceles ![]() is
is ![]() and its area is
and its area is ![]() . What is the length of one of the congruent sides?
. What is the length of one of the congruent sides?
![]()
Problem 15
Let ![]() and
and ![]() be numbers with
be numbers with ![]() . Which of the following is impossible?
. Which of the following is impossible?
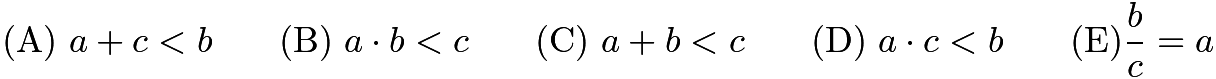
Problem 16
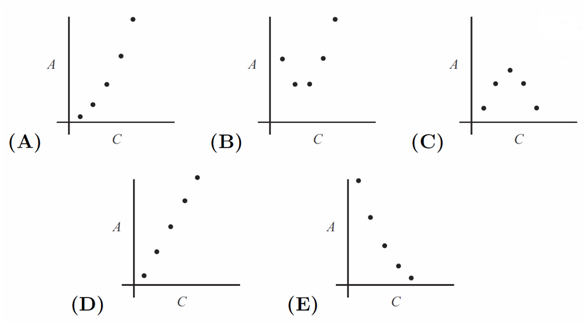
Amanda draws five circles with radii ![]() and
and ![]() . Then for each circle she plots the point
. Then for each circle she plots the point ![]() , where
, where ![]() is its circumference and
is its circumference and ![]() is its area. Which of the following could be her graph?
is its area. Which of the following could be her graph?
Problem 17
A mixture of ![]() liters of paint is
liters of paint is ![]() red tint,
red tint, ![]() yellow tint and
yellow tint and ![]() water. Five liters of yellow tint are added to the original mixture. What is the percent of yellow tint in the new mixture?
water. Five liters of yellow tint are added to the original mixture. What is the percent of yellow tint in the new mixture?
![]()
Problem 18
The product of the two ![]() -digit numbers
-digit numbers
![]() and
and ![]()
has thousands digit ![]() and units digit
and units digit ![]() . What is the sum of
. What is the sum of ![]() and
and ![]() ?
?
![]()
Problem 19
Pick two consecutive positive integers whose sum is less than ![]() . Square both of those integers and then find the difference of the squares. Which of the following could be the difference?
. Square both of those integers and then find the difference of the squares. Which of the following could be the difference?
![]()
Problem 20
Before district play, the Unicorns had won ![]() of their basketball games. During district play, they won six more games and lost two, to finish the season having won half their games. How many games did the Unicorns play in all?
of their basketball games. During district play, they won six more games and lost two, to finish the season having won half their games. How many games did the Unicorns play in all?
![]()
Problem 21
Two cards are dealt from a deck of four red cards labeled ![]() and four green cards labeled
and four green cards labeled ![]() . A winning pair is two of the same color or two of the same letter. What is the probability of drawing a winning pair?
. A winning pair is two of the same color or two of the same letter. What is the probability of drawing a winning pair?
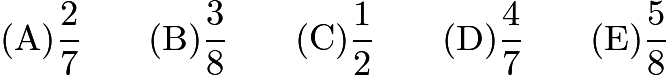
Problem 22
A lemming sits at a corner of a square with side length ![]() meters. The lemming runs
meters. The lemming runs ![]() meters along a diagonal toward the opposite corner. It stops, makes a
meters along a diagonal toward the opposite corner. It stops, makes a ![]() degree right turn and runs
degree right turn and runs ![]() more meters. A scientist measures the shortest distance between the lemming and each side of the square. What is the average of these four distances in meters?
more meters. A scientist measures the shortest distance between the lemming and each side of the square. What is the average of these four distances in meters?
![]()
Problem 23
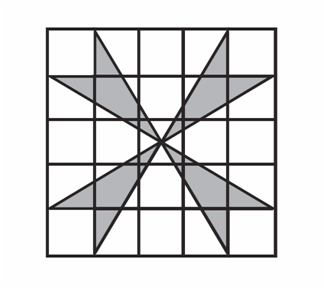
What is the area of the shaded part shown in the ![]() x
x ![]() grid?
grid?
Problem 24
A bag contains four pieces of paper, each labeled with one of the digits "1, 2, 3" or "4", with no repeats. Three of these pieces are drawn, one at a time without replacement, to construct a three-digit number. What is the probability that the three-digit number is a multiple of 3?
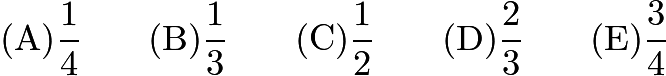
Problem 25
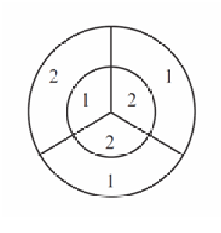
On the dart board shown in the Figure, the outer circle has radius ![]() and the inner circle has a radius of 3. Three radii divide each circle into three congruent regions, with point values shown. The probability that a dart will hit a given region is proportional to the area of the region. When two darts hit this board, the score is the sum of the point values in the regions. What is the probability that the score is odd?
and the inner circle has a radius of 3. Three radii divide each circle into three congruent regions, with point values shown. The probability that a dart will hit a given region is proportional to the area of the region. When two darts hit this board, the score is the sum of the point values in the regions. What is the probability that the score is odd?
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1