- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
2006 AMC 8 真题与答案及免费中文视频详解(翰林独家)
2006 AMC 8 Problems & Solutions
2006 AMC 8 真题与答案及中文视频详解(翰林独家)
Problem 1
Mindy made three purchases for ![]() ,
, ![]() , and
, and ![]() . What was her total, to the nearest dollar?
. What was her total, to the nearest dollar?
![]()
Problem 2
On the AMC 8 contest Billy answers 13 questions correctly, answers 7 questions incorrectly and doesn't answer the last 5. What is his score?
![]()
Problem 3
Elisa swims laps in the pool. When she first started, she completed 10 laps in 25 minutes. Now she can finish 12 laps in 24 minutes. By how many minutes has she improved her lap time?
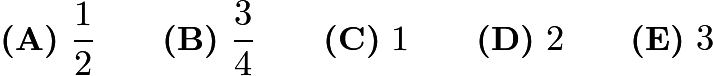
Problem 4
Initially, a spinner points west. Chenille moves it clockwise 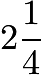 revolutions and then counterclockwise
revolutions and then counterclockwise 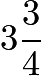 revolutions. In what direction does the spinner point after the two moves?
revolutions. In what direction does the spinner point after the two moves?
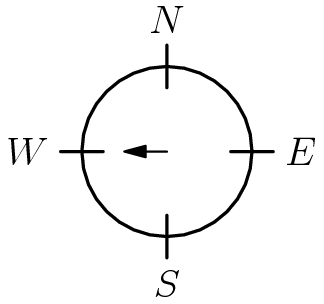
![]()
Problem 5
Points ![]() and
and ![]() are midpoints of the sides of the larger square. If the larger square has area 60, what is the area of the smaller square?
are midpoints of the sides of the larger square. If the larger square has area 60, what is the area of the smaller square?
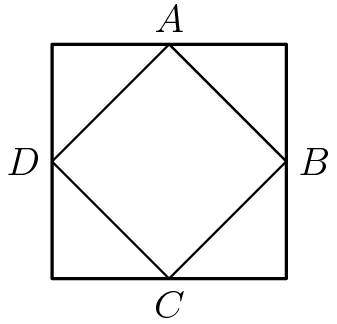
![]()
Problem 6
The letter T is formed by placing two ![]() inch rectangles next to each other, as shown. What is the perimeter of the T, in inches?
inch rectangles next to each other, as shown. What is the perimeter of the T, in inches?
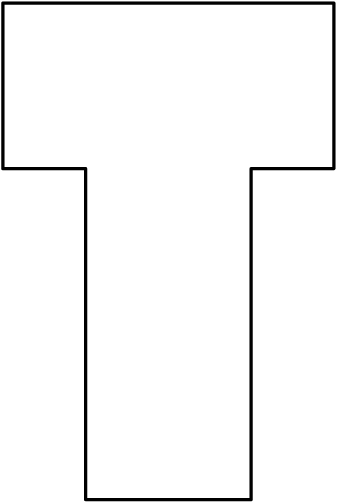
![]()
Problem 9
What is the product of  ?
?
![]()
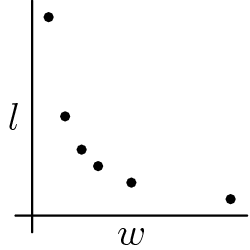
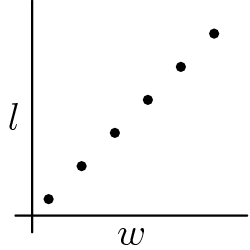
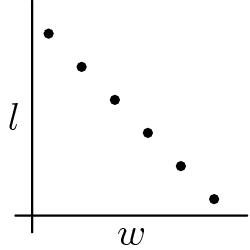
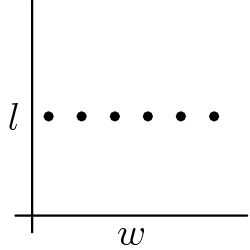
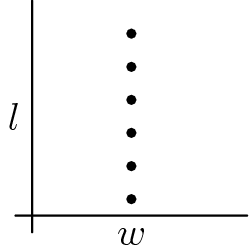
Problem 10
Jorge's teacher asks him to plot all the ordered pairs 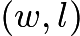 of positive integers for which
of positive integers for which 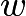 is the width and
is the width and 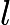 is the length of a rectangle with area 12. What should his graph look like?
is the length of a rectangle with area 12. What should his graph look like?
![]()
![]()
![]()
![]()
![]()
Problem 11
How many two-digit numbers have digits whose sum is a perfect square?
![]()
Problem 12
Antonette gets ![]() on a 10-problem test,
on a 10-problem test, ![]() on a 20-problem test and
on a 20-problem test and ![]() on a 30-problem test. If the three tests are combined into one 60-problem test, which percent is closest to her overall score?
on a 30-problem test. If the three tests are combined into one 60-problem test, which percent is closest to her overall score?
![]()
Problem 13
Cassie leaves Escanaba at 8:30 AM heading for Marquette on her bike. She bikes at a uniform rate of 12 miles per hour. Brian leaves Marquette at 9:00 AM heading for Escanaba on his bike. He bikes at a uniform rate of 16 miles per hour. They both bike on the same 62-mile route between Escanaba and Marquette. At what time in the morning do they meet?
![]()
Problem 14
Problems 14, 15 and 16 involve Mrs. Reed's English assignment.
A Novel Assignment
The students in Mrs. Reed's English class are reading the same 760-page novel. Three friends, Alice, Bob and Chandra, are in the class. Alice reads a page in 20 seconds, Bob reads a page in 45 seconds and Chandra reads a page in 30 seconds.
If Bob and Chandra both read the whole book, Bob will spend how many more seconds reading than Chandra?
![]()
Problem 15
Problems 14, 15 and 16 involve Mrs. Reed's English assignment.
A Novel Assignment
The students in Mrs. Reed's English class are reading the same 760-page novel. Three friends, Alice, Bob and Chandra, are in the class. Alice reads a page in 20 seconds, Bob reads a page in 45 seconds and Chandra reads a page in 30 seconds.
Chandra and Bob, who each have a copy of the book, decide that they can save time by "team reading" the novel. In this scheme, Chandra will read from page 1 to a certain page and Bob will read from the next page through page 760, finishing the book. When they are through they will tell each other about the part they read. What is the last page that Chandra should read so that she and Bob spend the same amount of time reading the novel?
![]()
Problem 16
Problems 14, 15 and 16 involve Mrs. Reed's English assignment.
A Novel Assignment
The students in Mrs. Reed's English class are reading the same 760-page novel. Three friends, Alice, Bob and Chandra, are in the class. Alice reads a page in 20 seconds, Bob reads a page in 45 seconds and Chandra reads a page in 30 seconds.
Before Chandra and Bob start reading, Alice says she would like to team read with them. If they divide the book into three sections so that each reads for the same length of time, how many seconds will each have to read?
![]()
Problem 17
Jeff rotates spinners ![]() ,
, ![]() and
and ![]() and adds the resulting numbers. What is the probability that his sum is an odd number?
and adds the resulting numbers. What is the probability that his sum is an odd number?
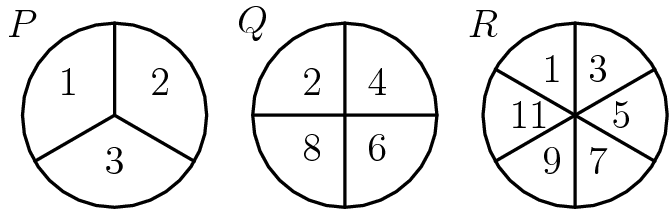
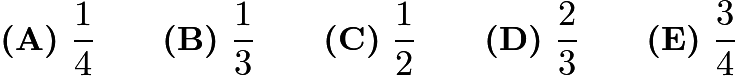
Problem 18
A cube with 3-inch edges is made using 27 cubes with 1-inch edges. Nineteen of the smaller cubes are white and eight are black. If the eight black cubes are placed at the corners of the larger cube, what fraction of the surface area of the larger cube is white?
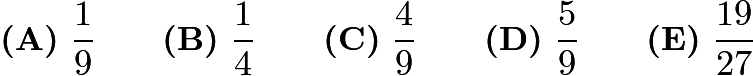
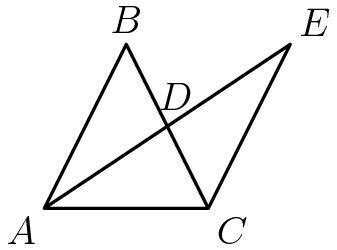
Problem 19
Triangle ![]() is an isosceles triangle with
is an isosceles triangle with ![]() . Point
. Point ![]() is the midpoint of both
is the midpoint of both ![]() and
and ![]() , and
, and ![]() is 11 units long. Triangle
is 11 units long. Triangle ![]() is congruent to triangle
is congruent to triangle ![]() . What is the length of
. What is the length of ![]() ?
?
![]()
Problem 20
A singles tournament had six players. Each player played every other player only once, with no ties. If Helen won 4 games, Ines won 3 games, Janet won 2 games, Kendra won 2 games and Lara won 2 games, how many games did Monica (the sixth player) win?
![]()
Problem 21
An aquarium has a rectangular base that measures ![]() cm by
cm by ![]() cm and has a height of
cm and has a height of ![]() cm. The aquarium is filled with water to a depth of
cm. The aquarium is filled with water to a depth of ![]() cm. A rock with volume
cm. A rock with volume ![]() is then placed in the aquarium and completely submerged. By how many centimeters does the water level rise?
is then placed in the aquarium and completely submerged. By how many centimeters does the water level rise?
![]()
Problem 22
Three different one-digit positive integers are placed in the bottom row of cells. Numbers in adjacent cells are added and the sum is placed in the cell above them. In the second row, continue the same process to obtain a number in the top cell. What is the difference between the largest and smallest numbers possible in the top cell?
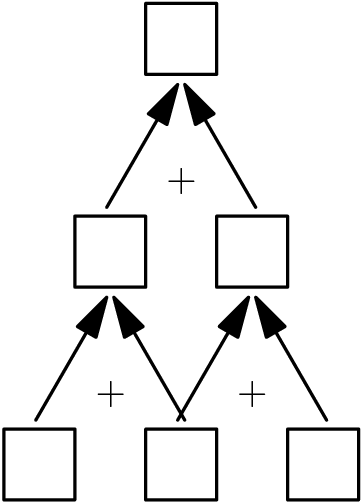
![]()
Problem 23
A box contains gold coins. If the coins are equally divided among six people, four coins are left over. If the coins are equally divided among five people, three coins are left over. If the box holds the smallest number of coins that meets these two conditions, how many coins are left when equally divided among seven people?
![]()
Problem 24
In the multiplication problem below ![]() ,
, ![]() ,
, ![]() ,
, ![]() and are different digits. What is
and are different digits. What is ![]() ?
?
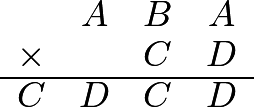
![]()
Problem 25
Barry wrote 6 different numbers, one on each side of 3 cards, and laid the cards on a table, as shown. The sums of the two numbers on each of the three cards are equal. The three numbers on the hidden sides are prime numbers. What is the average of the hidden prime numbers?
![]()
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





