- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
2012 AMC 8 真题与答案解析
2012 AMC 8真题
答案详细解析请参考文末
Problem 1
Rachelle uses ![]() pounds of meat to make
pounds of meat to make ![]() hamburgers for her family. How many pounds of meat does she need to make
hamburgers for her family. How many pounds of meat does she need to make ![]() hamburgers for a neighborhood picnic?
hamburgers for a neighborhood picnic?
![]()
Problem 2
In the country of East Westmore, statisticians estimate there is a baby born every ![]() hours and a death every day. To the nearest hundred, how many people are added to the population of East Westmore each year?
hours and a death every day. To the nearest hundred, how many people are added to the population of East Westmore each year?
![]()
Problem 3
On February 13 ![]() listed the length of daylight as 10 hours and 24 minutes, the sunrise was
listed the length of daylight as 10 hours and 24 minutes, the sunrise was ![]() , and the sunset as
, and the sunset as ![]() . The length of daylight and sunrise were correct, but the sunset was wrong. When did the sun really set?
. The length of daylight and sunrise were correct, but the sunset was wrong. When did the sun really set?
![]()
Problem 4
Peter's family ordered a 12-slice pizza for dinner. Peter ate one slice and shared another slice equally with his brother Paul. What fraction of the pizza did Peter eat?
![]()
Problem 5
In the diagram, all angles are right angles and the lengths of the sides are given in centimeters. Note the diagram is not drawn to scale. What is ![]() , in centimeters?
, in centimeters?
![[asy] pair A,B,C,D,E,F,G,H,I,J,K,L,M,N,O,P,Q,R; A=(4,0); B=(7,0); C=(7,4); D=(8,4); E=(8,5); F=(10,5); G=(10,7); H=(7,7); I=(7,8); J=(5,8); K=(5,7); L=(4,7); M=(4,6); N=(0,6); O=(0,5); P=(2,5); Q=(2,3); R=(4,3); draw(A--B--C--D--E--F--G--H--I--J--K--L--M--N--O--P--Q--R--cycle); label("$X$",(3.4,1.5)); label("6",(7.6,1.5)); label("1",(7.6,3.5)); label("1",(8.4,4.6)); label("2",(9.4,4.6)); label("2",(10.4,6)); label("3",(8.4,7.4)); label("1",(7.5,7.8)); label("2",(6,8.5)); label("1",(4.7,7.8)); label("1",(4.3,7.5)); label("1",(3.5,6.5)); label("4",(1.8,6.5)); label("1",(-0.5,5.5)); label("2",(0.8,4.5)); label("2",(1.5,3.8)); label("2",(2.8,2.6));[/asy]](http://latex.artofproblemsolving.com/b/c/d/bcd57a9d78159bce4d3873f81f5d879beaed1d5a.png)
![]()
Problem 6
A rectangular photograph is placed in a frame that forms a border two inches wide on all sides of the photograph. The photograph measures 8 inches high and 10 inches wide. What is the area of the border, in square inches?
![]()
Problem 7
Isabella must take four 100-point tests in her math class. Her goal is to achieve an average grade of 95 on the tests. Her first two test scores were 97 and 91. After seeing her score on the third test, she realized she can still reach her goal. What is the lowest possible score she could have made on the third test?
![]()
Problem 8
A shop advertises everything is "half price in today's sale." In addition, a coupon gives a 20% discount on sale prices. Using the coupon, the price today represents what percentage off the original price?
![]()
Problem 9
The Fort Worth Zoo has a number of two-legged birds and a number of four-legged mammals. On one visit to the zoo, Margie counted 200 heads and 522 legs. How many of the animals that Margie counted were two-legged birds?
![]()
Problem 10
How many 4-digit numbers greater than 1000 are there that use the four digits of 2012?
![]()
Problem 11
The mean, median, and unique mode of the positive integers 3, 4, 5, 6, 6, 7, and ![]() are all equal. What is the value of
are all equal. What is the value of ![]() ?
?
![]()
Problem 12
What is the units digit of ![]() ?
?
![]()
Problem 13
Jamar bought some pencils costing more than a penny each at the school bookstore and paid ![]() . Sharona bought some of the same pencils and paid
. Sharona bought some of the same pencils and paid ![]() . How many more pencils did Sharona buy than Jamar?
. How many more pencils did Sharona buy than Jamar?
![]()
Problem 14
In the BIG N, a middle school football conference, each team plays every other team exactly once. If a total of 21 conference games were played during the 2012 season, how many teams were members of the BIG N conference?
![]()
Problem 15
The smallest number greater than 2 that leaves a remainder of 2 when divided by 3, 4, 5, or 6 lies between what numbers?
![]()
Problem 16
Each of the digits 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9 is used only once to make two five-digit numbers so that they have the largest possible sum. Which of the following could be one of the numbers?
![]()
Problem 17
A square with integer side length is cut into 10 squares, all of which have integer side length and at least 8 of which have area 1. What is the smallest possible value of the length of the side of the original square?
![]()
Problem 18
What is the smallest positive integer that is neither prime nor square and that has no prime factor less than 50?
![]()
Problem 19
In a jar of red, green, and blue marbles, all but 6 are red marbles, all but 8 are green, and all but 4 are blue. How many marbles are in the jar?
![]()
Problem 20
What is the correct ordering of the three numbers ![]() ,
, ![]() , and
, and ![]() , in increasing order?
, in increasing order?
![]()
![]()
Problem 21
Marla has a large white cube that has an edge of 10 feet. She also has enough green paint to cover 300 square feet. Marla uses all the paint to create a white square centered on each face, surrounded by a green border. What is the area of one of the white squares, in square feet?
![]()
Problem 22
Let ![]() be a set of nine distinct integers. Six of the elements are 2, 3, 4, 6, 9, and 14. What is the number of possible values of the median of
be a set of nine distinct integers. Six of the elements are 2, 3, 4, 6, 9, and 14. What is the number of possible values of the median of ![]() ?
?
![]()
Problem 23
An equilateral triangle and a regular hexagon have equal perimeters. If the area of the triangle is 4, what is the area of the hexagon?
![]()
Problem 24
A circle of radius 2 is cut into four congruent arcs. The four arcs are joined to form the star figure shown. What is the ratio of the area of the star figure to the area of the original circle?
![[asy] size(0,50); draw((-1,1)..(-2,2)..(-3,1)..(-2,0)..cycle); dot((-1,1)); dot((-2,2)); dot((-3,1)); dot((-2,0)); draw((1,0){up}..{left}(0,1)); dot((1,0)); dot((0,1)); draw((0,1){right}..{up}(1,2)); dot((1,2)); draw((1,2){down}..{right}(2,1)); dot((2,1)); draw((2,1){left}..{down}(1,0));[/asy]](http://latex.artofproblemsolving.com/4/f/e/4fe4633986b1f264beb80f6015661aef00c4f803.png)
![]()
Problem 25
A square with area 4 is inscribed in a square with area 5, with one vertex of the smaller square on each side of the larger square. A vertex of the smaller square divides a side of the larger square into two segments, one of length ![]() , and the other of length
, and the other of length ![]() . What is the value of
. What is the value of ![]() ?
?
![[asy] draw((0,2)--(2,2)--(2,0)--(0,0)--cycle); draw((0,0.3)--(0.3,2)--(2,1.7)--(1.7,0)--cycle); label("$a$",(-0.1,0.15)); label("$b$",(-0.1,1.15));[/asy]](http://latex.artofproblemsolving.com/3/d/4/3d4cdd3dbcabe3dc76b806d60b785416afc65f11.png)
![]()
- Since Rachelle uses
 pounds of meat to make
pounds of meat to make  hamburgers, she uses
hamburgers, she uses  pounds of meat to make one hamburger. She'll need 24 times that amount of meat for 24 hamburgers, or
pounds of meat to make one hamburger. She'll need 24 times that amount of meat for 24 hamburgers, or  .
. - There are
 births and one death everyday in East Westmore. Therefore, the population increases by
births and one death everyday in East Westmore. Therefore, the population increases by  -
-  =
=  people everyday. Thus, there are
people everyday. Thus, there are  people added to the population every year. Rounding, we find the answer is
people added to the population every year. Rounding, we find the answer is  .
. - The problem wants us to find the time of sunset and gives us the length of daylight and time of sunrise. So all we have to do is add the length of daylight to the time of sunrise to obtain the answer. Convert 10 hours and 24 minutes into
 in order to add easier.Adding, we find that the time of sunset is
in order to add easier.Adding, we find that the time of sunset is 
- Peter ate
 slices. The pizza has
slices. The pizza has  slices total. Taking the ratio of the amount of slices Peter ate to the amount of slices in the pizza, we find that Peter ate
slices total. Taking the ratio of the amount of slices Peter ate to the amount of slices in the pizza, we find that Peter ate  of the pizza.
of the pizza.  The figure is the same height on both sides, so the sum of the lengths contributing to the height on the left side will equal the sum of the lengths contributing to the height on the left side.
The figure is the same height on both sides, so the sum of the lengths contributing to the height on the left side will equal the sum of the lengths contributing to the height on the left side. Thus, the answer is
Thus, the answer is  .
.- First, we start with a sketch. It's always a good idea to start with a picture, although not as detailed as this one. (Tip: On the actual AMC 8 test, you should NOT color your picture in, even if it is beautiful)
 In order to find the area of the frame, we need to subtract the area of the photograph from the area of the photograph and the frame together. The area of the photograph is
In order to find the area of the frame, we need to subtract the area of the photograph from the area of the photograph and the frame together. The area of the photograph is  square inches. The height of the whole frame (including the photograph) would be
square inches. The height of the whole frame (including the photograph) would be  , and the width of the whole frame,
, and the width of the whole frame,  . Therefore, the area of the whole figure would be
. Therefore, the area of the whole figure would be square inches. Subtracting the area of the photograph from the area of both the frame and photograph, we find the answer to be
square inches. Subtracting the area of the photograph from the area of both the frame and photograph, we find the answer to be  .
. - Isabella wants an average grade of
 on her 4 tests; this also means that she wants the sum of her test scores to be at least
on her 4 tests; this also means that she wants the sum of her test scores to be at least  (if she goes over this number, she'll be over her goal!). She's already taken two tests, which sum to
(if she goes over this number, she'll be over her goal!). She's already taken two tests, which sum to  , which means she needs
, which means she needs  more points to achieve her desired average. In order to minimize the score on the third test, we assume that Isabella will receive all
more points to achieve her desired average. In order to minimize the score on the third test, we assume that Isabella will receive all  points on the fourth test. Therefore, the lowest Isabella could have scored on the third test would be
points on the fourth test. Therefore, the lowest Isabella could have scored on the third test would be  .
. - Let the original price of an item be
 .First, everything is half-off, so the price is now
.First, everything is half-off, so the price is now  .Next, the extra coupon applies 20% off on the sale price, so the price after this discount will be
.Next, the extra coupon applies 20% off on the sale price, so the price after this discount will be  of what it was before. (Notice how this is not applied to the original price; if it were, the solution would be applying 50% + 20 % = 70% off the original price.)
of what it was before. (Notice how this is not applied to the original price; if it were, the solution would be applying 50% + 20 % = 70% off the original price.) The price of the item after all discounts have been applied is
The price of the item after all discounts have been applied is  . However, we need to find the percentage off the original price, not the current percentage of the original price. We then subtract
. However, we need to find the percentage off the original price, not the current percentage of the original price. We then subtract  from
from  (the original price of the item), to find the answer,
(the original price of the item), to find the answer,  .
. - Let the number of two-legged birds be
 and the number of four-legged mammals be
and the number of four-legged mammals be  . We can now use systems of equations to solve this problem.Write two equations:
. We can now use systems of equations to solve this problem.Write two equations:
 Now multiply the latter equation by
Now multiply the latter equation by  .
.
 By subtracting the second equation from the first equation, we find that
By subtracting the second equation from the first equation, we find that  . Since there were
. Since there were  heads, meaning that there were
heads, meaning that there were  animals, there were
animals, there were  two-legged birds.
two-legged birds. - For this problem, all we need to do is find the amount of valid 4-digit numbers that can be made from the digits of
 , since all of the valid 4-digit number will always be greater than
, since all of the valid 4-digit number will always be greater than  . The best way to solve this problem is by using casework.There can be only two leading digits, namely
. The best way to solve this problem is by using casework.There can be only two leading digits, namely  or
or  .When the leading digit is
.When the leading digit is  , you can make
, you can make  such numbers.When the leading digit is
such numbers.When the leading digit is  , you can make
, you can make  such numbers.Summing the amounts of numbers, we find that there are
such numbers.Summing the amounts of numbers, we find that there are  such numbers.
such numbers. - Since there must be a unique mode, and
 is already repeated twice,
is already repeated twice,  cannot be any of the numbers already listed (3, 4, 5, 7). (If it were, the mode would not be unique.) So
cannot be any of the numbers already listed (3, 4, 5, 7). (If it were, the mode would not be unique.) So  must be
must be  , or a new number.We can eliminate answer choices
, or a new number.We can eliminate answer choices  and
and  , because of the above statement. Now we need to test the remaining answer choices.Case 1:
, because of the above statement. Now we need to test the remaining answer choices.Case 1:  Mode:
Mode:  Median:
Median:  Mean:
Mean:  Since the mean does not equal the median or mode,
Since the mean does not equal the median or mode,  can also be eliminated.Case 2:
can also be eliminated.Case 2:  Mode:
Mode:  Median:
Median:  Mean:
Mean:  We are done with this problem, because we have found when
We are done with this problem, because we have found when  , the condition is satisfied. Therefore, the answer is
, the condition is satisfied. Therefore, the answer is  .
. - The problem wants us to find the units digit of
 , therefore, we can eliminate the tens digit of
, therefore, we can eliminate the tens digit of  , because the tens digit will not affect the final result. So our new expression is
, because the tens digit will not affect the final result. So our new expression is  . Now we need to look for a pattern in the units digit.
. Now we need to look for a pattern in the units digit.



 We observe that there is a pattern for the units digit which recurs every four powers of three. Using this pattern, we can subtract 1 from 2012 and divide by 4. The remainder is the power of three that we are looking for, plus one.
We observe that there is a pattern for the units digit which recurs every four powers of three. Using this pattern, we can subtract 1 from 2012 and divide by 4. The remainder is the power of three that we are looking for, plus one.  divided by
divided by  leaves a remainder of
leaves a remainder of  , so the answer is the units digit of
, so the answer is the units digit of  , or
, or  . Thus, we find that the units digit of
. Thus, we find that the units digit of  is
is .
. - We assume that the price of the pencils remains constant. Convert
 and
and  to cents. Since the price of the pencils is more than one penny, we can find the price of one pencil (in cents) by taking the greatest common divisor of
to cents. Since the price of the pencils is more than one penny, we can find the price of one pencil (in cents) by taking the greatest common divisor of  and
and  , which is
, which is  . Therefore, Jamar bought
. Therefore, Jamar bought  pencils and Sharona bought
pencils and Sharona bought  pencils. Thus, Sharona bought
pencils. Thus, Sharona bought  more pencils than Jamar.
more pencils than Jamar. - This problem is very similar to a handshake problem. We use the formula
 to usually find the number of games played (or handshakes). Now we have to use the formula in reverse.So we have the equation
to usually find the number of games played (or handshakes). Now we have to use the formula in reverse.So we have the equation  . Solving, we find that the number of teams in the BIG N conference is
. Solving, we find that the number of teams in the BIG N conference is  .
. - To find the answer to this problem, we need to find the least common multiple of
 ,
,  ,
,  ,
,  and add
and add  to the result. The least common multiple of the four numbers is
to the result. The least common multiple of the four numbers is  , and by adding
, and by adding  , we find that that such number is
, we find that that such number is  . Now we need to find the only given range that contains
. Now we need to find the only given range that contains  . The only such range is answer
. The only such range is answer  , and so our final answer is
, and so our final answer is  .
. - In order to maximize the sum of the numbers, the numbers must have their digits ordered in decreasing value. There are only two numbers from the answer choices with this property:
 and
and  . To determine the answer we will have to use estimation and the first two digits of the numbers.For
. To determine the answer we will have to use estimation and the first two digits of the numbers.For  the number that would maximize the sum would start with
the number that would maximize the sum would start with  . The first two digits of
. The first two digits of  (when rounded) are
(when rounded) are  . Adding
. Adding  and
and  , we find that the first three digits of the sum of the two numbers would be
, we find that the first three digits of the sum of the two numbers would be  .For
.For  the number that would maximize the sum would start with
the number that would maximize the sum would start with  . The first two digits of
. The first two digits of  (when rounded) are
(when rounded) are  . Adding
. Adding  and
and  , we find that the first three digits of the sum of the two numbers would be
, we find that the first three digits of the sum of the two numbers would be  .From the estimations, we can say that the answer to this problem is
.From the estimations, we can say that the answer to this problem is  .
. - The first answer choice
 , can be eliminated since there must be
, can be eliminated since there must be  squares with integer side lengths. We then test the next largest sidelength which is
squares with integer side lengths. We then test the next largest sidelength which is  . The square with area
. The square with area  can be partitioned into
can be partitioned into  squares with area
squares with area  and two squares with area
and two squares with area  , which satisfies all the conditions of the problem. Therefore, the smallest possible value of the length of the side of the original square is
, which satisfies all the conditions of the problem. Therefore, the smallest possible value of the length of the side of the original square is  .
. - The problem states that the answer cannot be a perfect square or have prime factors less than
 . Therefore, the answer will be the product of at least two different primes greater than
. Therefore, the answer will be the product of at least two different primes greater than  . The two smallest primes greater than
. The two smallest primes greater than  are
are  and
and  . Multiplying these two primes, we obtain the number
. Multiplying these two primes, we obtain the number  , which is also the smallest number on the list of answer choices. So we are done, and the answer is
, which is also the smallest number on the list of answer choices. So we are done, and the answer is  .
. - Let
 be the number of red marbles,
be the number of red marbles,  be the number of green marbles, and
be the number of green marbles, and  be the number of blue marbles.If "all but 6 are red marbles", that means that the number of green marbles and the number of blue marbles amount to
be the number of blue marbles.If "all but 6 are red marbles", that means that the number of green marbles and the number of blue marbles amount to  . Likewise, the number of red marbles and blue marbles amount to
. Likewise, the number of red marbles and blue marbles amount to  , and the number of red marbles and the number of green marbles amount to
, and the number of red marbles and the number of green marbles amount to  .We have three equations:
.We have three equations:

 We add all the equations to obtain a fourth equation:
We add all the equations to obtain a fourth equation: Now divide by
Now divide by  on both sides to find the total number of marbles:
on both sides to find the total number of marbles: Since the sum of the number of red marbles, green marbles, and blue marbles is the number of marbles in the jar, the total number of marbles in the jar is
Since the sum of the number of red marbles, green marbles, and blue marbles is the number of marbles in the jar, the total number of marbles in the jar is  .Notice how we never knew how many of each color there were (there is 1 green marble, 5 blue marbles, and 3 red marbles).
.Notice how we never knew how many of each color there were (there is 1 green marble, 5 blue marbles, and 3 red marbles). - The value of
 is
is  . Now we give all the fractions a common denominator.
. Now we give all the fractions a common denominator.

 Ordering the fractions from least to greatest, we find that they are in the order listed. Therefore, our final answer is
Ordering the fractions from least to greatest, we find that they are in the order listed. Therefore, our final answer is  .
. - If Marla evenly distributes her
 square feet of paint between the 6 faces, each face will get
square feet of paint between the 6 faces, each face will get square feet of paint. The surface area of one of the faces of the cube is
square feet of paint. The surface area of one of the faces of the cube is  square feet. Therefore, there will be
square feet. Therefore, there will be  square feet of white on each side.
square feet of white on each side. - First, we find that the minimum value of the median of
 will be
will be  .We then experiment with sequences of numbers to determine other possible medians.Median:
.We then experiment with sequences of numbers to determine other possible medians.Median:  Sequence:
Sequence:  Median:
Median:  Sequence:
Sequence:  Median:
Median:  Sequence:
Sequence:  Median:
Median:  Sequence:
Sequence:  Median:
Median:  Sequence:
Sequence:  Median:
Median:  Sequence:
Sequence: 
Median:

Sequence:

Any number greater than
 also cannot be a median of set
also cannot be a median of set  .
.There are then
 possible medians of set
possible medians of set  .
. - Let the perimeter of the equilateral triangle be
 . The side length of the equilateral triangle would then be
. The side length of the equilateral triangle would then be  and the sidelength of the hexagon would be
and the sidelength of the hexagon would be  .A hexagon contains six equilateral triangles. One of these triangles would be similar to the large equilateral triangle in the ratio
.A hexagon contains six equilateral triangles. One of these triangles would be similar to the large equilateral triangle in the ratio  , since the sidelength of the small equilateral triangle is half the sidelength of the large one. Thus, the area of one of the small equilateral triangles is
, since the sidelength of the small equilateral triangle is half the sidelength of the large one. Thus, the area of one of the small equilateral triangles is  . The area of the hexagon is then
. The area of the hexagon is then  .
. ![[asy] dot((0,0),red); dot((0,2),red); dot((2,0),red); dot((2,2),red); draw((0,0)--(0,2)--(2,2)--(2,0)--cycle,red); size(0,50); draw((1,0){up}..{left}(0,1)); dot((1,0)); dot((0,1)); draw((0,1){right}..{up}(1,2)); dot((1,2)); draw((1,2){down}..{right}(2,1)); dot((2,1)); draw((2,1){left}..{down}(1,0));[/asy]](http://latex.artofproblemsolving.com/e/7/a/e7a51fd3bfbbc2e3c43ef157486d1bf10c57a6f9.png) Draw a square around the star figure. The sidelength of this square is
Draw a square around the star figure. The sidelength of this square is  , because the sidelength is the diameter of the circle. The square forms
, because the sidelength is the diameter of the circle. The square forms  -quarter circles around the star figure. This is the equivalent of one large circle with radius
-quarter circles around the star figure. This is the equivalent of one large circle with radius  , meaning that the total area of the quarter circles is
, meaning that the total area of the quarter circles is  . The area of the square is
. The area of the square is  . Thus, the area of the star figure is
. Thus, the area of the star figure is  . The area of the circle is
. The area of the circle is  . Taking the ratio of the two areas, we find the answer is
. Taking the ratio of the two areas, we find the answer is  .
.- The total area of the four congruent triangles formed by the squares is
 . Therefore, the area of one of these triangles is
. Therefore, the area of one of these triangles is  . The height of one of these triangles is
. The height of one of these triangles is  and the base is
and the base is  . Using the formula for area of the triangle, we have
. Using the formula for area of the triangle, we have  . Multiply by
. Multiply by  on both sides to find that the value of
on both sides to find that the value of  is
is 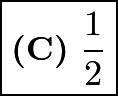 .
.
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





