历年 Canadian Open Mathematics Challenge加拿大数学公开赛

真题与答案下载

翰林国际教育全网首发

力争超快速发布最全资料

助你在升学路上一帆风顺

为你

千千万万遍

2000 COMC真题答案免费下载

共计2.5小时考试时间

此套试卷由两部分题目组成

Part A共8题，每题5分

Part B共4题，每题10分

共计12题，满分80分

不可使用任何计算器

完整版下载链接见文末

部分真题预览：

Part A Solutions:

A2) The terms in the sequence are paired, by combining each odd-numbered term with the next term (that is, we combine terms 1 and 2, 3 and 4, 5 and 6, etc).
The sum of each of these pairs is 9.
So we need 20 of these pairs to reach a sum of 180.
Thus we need 2 × 20 or 40 terms.
ANSWER: 40

Part B Solutions:

B3)

1. We first consider Alphonse’s possible moves to begin the game. We can assume, without loss of generality, that he cuts on the left side of the black triangle.
   1. Case 1:Alphonse removes two white triangles, leaving .
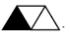      In this case, Beryl removes only one white triangle, and passes the shape back to Alphonse, forcing him to remove the last white triangle and lose.
   2. Case 2:Alphonse removes one white triangle only, leaving .
      Beryl removes both of the white triangles on the right, leaving Alphonse in the same position as in Case 1 for his second turn.
      Therefore Beryl can always win, regardless of Alphonse’s strategy.
2. We show that, again, Beryl always has a winning strategy.
   The strategy is to reduce the shape in Figure 2 to the shape in Figure 1, and to have Alphonse make the first cut at this stage. Beryl also knows that if she is forced into a position of being the first to cut when Figure 2 is reduced to Figure 1, then Alphonse can force her to lose.
   We number the lines on the diagram for convenience.
   
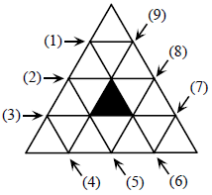
   We can assume without loss of generality (because of symmetry) that Beryl cuts along (1), (2) or (3) to begin.
   If she cuts (2) or (3), then Alphonse cuts the other of these two and leaves Beryl with Figure 1, where she will lose.
   Therefore Beryl cuts (1) to begin.
   If Alphonse now cuts (2) or (3), Beryl cuts the other of these two and passes the shape in Figure 1 back to Alphonse, and so he loses.
   If Alphonse cuts (8) or (9), Beryl cuts the opposite and passes the shape in Figure 1 to Alphonse, and so he loses. (Similarly, if he cuts (5) or (6)).
   So assume that Alphonse cuts (4) or (7), say (4) by symmetry.
   If Beryl now cuts any of (2), (3), (5), (6), (8), or (9), then Alphonse can force Beryl to lose, in the same way as she could have forced him to lose, as above. So Beryl cuts (7).
   Now Alphonse is forced to cut one of (2), (3), (5), (6), (8), or (9), and so Beryl makes the appropriate cut, passing the shape in Figure 1 back to Alphonse, and so he must lose.
   Therefore Beryl always can have a winning strategy.

 

完整版真题下载链接请注册或登录后查看

文件为PDF格式

推荐使用电脑下载

 

2000 COMC加拿大数学奥赛完整版真题免费下载

请点击下方链接访问

2000 COMC真题题目

 

如需打包下载，请联系小助手了解更多

翰林学员全站资料免费打包下载，专享高速下载通道。