历年 Canadian Open Mathematics Challenge加拿大数学公开赛

真题与答案下载

翰林国际教育全网首发

力争超快速发布最全资料

助你在升学路上一帆风顺

为你

千千万万遍

2003 COMC真题免费下载

共计2.5小时考试时间

此套试卷由两部分题目组成

Part A共8题，每题5分

Part B共4题，每题10分

共计12题，满分80分

不可使用任何计算器

完整版下载链接见文末

部分真题预览：

Part A :

1)Jeff, Gareth and Ina all share the same birthday. Gareth is one year older than Jeff, and Ina is two years older than Gareth. This year the sum of their ages is 118. How old is Gareth?

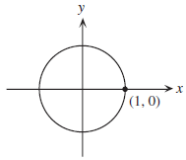
3)A circle of radius 1 is centred at the origin. Two particles start moving at the same time from the point (1 ,0) and move around the circle in opposite directions. One of the particles moves counterclockwise with constant speed v and the other moves clockwise with constant speed 3v. After leaving (1 ,0), the two particles meet first at point P, and continue until they meet next at point Q. Determine the coordinates of the point Q.

5)In the diagram, square ABCD has a side length of 6. Circular arcs of radius 6 are drawn with centres B and D. What is the area of the shaded region?

Part B :

2)A barn has a foundation in the shape of a trapezoid, with three sides of length 6 m, and one side of length 12 m, as shown.

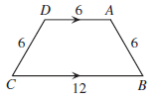
1. Determine each of the interior angles in the trapezoid.
2. Chuck the Llama is attached by a chain to a point on the outside wall of the barn. Chuck is smarter than the average llama, and so realizes that he can always reach the area between the barn and where the chain is fully extended.
   • If Chuck is attached at the point A with a chain of length 8 m, what is the area outside the barn that Chuck can reach?
   • If Chuck is attached at some point P along the wall between A and B with a chain of length 15 m, determine the location of P which restricts Chuck to the minimum area.

完整版真题下载链接请注册或登录后查看

文件为PDF格式

推荐使用电脑下载

 

2003 COMC加拿大数学奥赛完整版答案免费下载

请持续关注，稍后更新

 

如需打包下载，请联系小助手了解更多

翰林学员全站资料免费打包下载，专享高速下载通道。