- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
2005COMC加拿大数学公开赛真题免费下载
历年 Canadian Open Mathematics Challenge加拿大数学公开赛
真题与答案下载
翰林国际教育全网首发
力争超快速发布最全资料
助你在升学路上一帆风顺
为你
千千万万遍
2005 COMC真题免费下载
共计2.5小时考试时间
此套试卷由两部分题目组成
Part A共8题,每题5分
Part B共4题,每题10分
共计12题,满分80分
不可使用任何计算器
完整版下载链接见文末
部分真题预览:
Part A :
5)An office building has 50 storeys, 25 of which are painted black and the other 25 of which are painted gold. If the number of gold storeys in the top half of the building is added to the number of black storeys in the bottom half of the building, the sum is 28. How many gold storeys are there in the top half of the building?
6)In the grid shown, each row has a value assigned to it and each column has a value assigned to it. The number in each cell is the sum of its row and column values. For example, the “8” is the sum of the value assigned to the 3rd row and the value assigned to the 4th column. Determine the values of x and y.
7)In the diagram, the semi-circle has centre O and diameter AB. A ray of light leaves point P in a direction perpendicular to AB. It bounces off the semi-circle at point D in such a way that ∠PDO = ∠EDO. (In other words, the angle of incidence equals
the angle of reflection at D.) The ray DE then bounces off the circle in a similar
way at E before finally hitting the semicircle again at B. Determine \DOP.
Part B :
1)Piotr places numbers on a 3 by 3 grid using the following rule, called “Piotr’s Principle”:
For any three adjacent numbers in a horizontal, vertical or diagonal line, the middle number is always the average (mean) of its two neighbours.
- Using Piotr’s principle, determine the missing numbers in the grid to the right. (You should fill in the missing numbers in the grid in your answer booklet.)
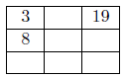
- Determine, with justification, the total of the nine numbers when the grid to the right is completed using Piotr’s Principle.
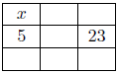
- Determine, with justification, the values of x and y when the grid to the right is completed using Piotr’s Principle.
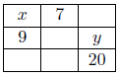
3)
- In the diagram, trapezoid ABCD has parallel sides AB and DC of lengths 10 and 20, respectively. Also, the length of AD is 6 and the length of BC is 8. Determine the area of trapezoid ABCD.

- In the diagram, PQRS is a rectangle and T is the midpoint of RS. The inscribed circles of 4PTS and 4RTQ each have radius 3. The inscribed circle of 4QPT has radius 4. Determine the dimensions of rectangle PQRS.

2005 COMC加拿大数学奥赛完整版答案免费下载
请持续关注,稍后更新
完整版真题资料可以底部二维码免费领取↓↓↓
翰林学员全站资料免费打包下载,专享高速下载通道。
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





